
Ellära
Om elektricitet
Grunden till elektricitet är materias egenskap att kunna lagra elektrisk laddning och den elektrostatiska kraftverkan som kan uppstå mellan laddade partiklar. Denna elektrostatiska kraft kallas coulombkraften och kan jämföras med gravitationskraften inom mekaniken. Ett klassiskt exempel på elektrostatisk kraftverkan är då man gnider en glasstav mot ett stycke sidentyg och placerar glasstaven i ett vridbart stativ. När sidentyget sedan förs mot glasstaven, kommer staven att dras mot tyget. Gnider man två glasstavar mot sidenstycket och placerar dem i stativ, kommer stavarna att vridas ifrån varandra när stativen flyttas ihop.
Elektricitet består av rörliga laddningar, som kan vara positiva eller negativa. Lika laddningar stöter bort, repellerar, varandra, medan olika laddningar drar till sig, attraherar, varandra. Material har olika bra elektrisk ledningsförmåga. I vissa material kan laddningar röra sig lätt och bilda en elektrisk ström, medan i andra material förflyttar sig laddningar dåligt och fungerar istället som isolatorer. Koppar är ett exempel på ett material med god ledningsförmåga. Plast har däremot dålig ledningsförmåga, och är exempel på ett isolerande material. Hur god ledningsförmåga ett ämne har beror på dess atomstruktur. Om atomerna har löst bundna elektroner kan de överföras till material vars atomer har underskott på elektroner. I exemplet med glasstavarna får sidentyget ett överskott av elektroner och blir negativt laddat, stavarna i sin tur blir positivt laddade. Det sker en omfördelning av laddningar, och betraktar man glasstavarna och sidentyget som ett slutet system kan man konstatera att det i systemet inte tillkommit eller försvunnit några laddningar. Detta är fundamentalt: den totala laddningen inom ett isolerat system kan aldrig förändras.
Elektriska storheter
Elektrisk laddning (Q, q)
Elektrisk laddning betecknas med bokstaven Q, enhetsladdningar brukar anges med lilla bokstaven q. Enheten för elektrisk laddning är en coulomb (1 C). En coulomb är lika med en ampere-sekund, 1 C = 1 As. I eltekniska sammanhang används ofta enheten amperetimmar (Ah), och inom kemin används elementarladdningen (e). Det finns två typer av elektrisk laddning – positiv och negativ. Ett material är negativt laddat om det har ett överskott av elektroner, och positivt laddat om det har överskott av protoner (= underskott av elektroner). Laddade partiklar ger upphov till ett elektriskt fält.
Elektriska dipolmoment (p)
Alla material påverkas av elektriska fält, även icke-metaller gör det, med den skillnaden att icke-metallernas atomer har starkare bundna elektroner och saknar fria, rörliga elektroner, s.k. valenselektroner. Materialen benämnes dielektriska material. I det ideala fallet är ett sådant material en isolator, som, i motsats till metaller, saknar egenskapen att leda ström. Dock, har många icke-metalliska material förmågan att reducera ett yttre statiskt fält, vilket beror på att elektroner och protoner påverkas av motsatt riktade krafter då materialet utsätts för ett yttre elektriskt fält. Laddningarna är fortfarande kvar i atomen, men effekten blir att atomen "tänjs ut", så att en positiv och en negativ pol bildas - en elektrisk dipol. Atomen kommer fortfarande att vara neutral, men den lilla förskjutningen av positivt och negativt ger upphov till elektriska effekter som beskrivs med ett elektriskt dipolmoment, en vektor som betecknas med lilla bokstaven p.
Elektriska dipolmoment förekommer i många ämnen redan utan ett yttre elektriskt fält. Laddningsförskjutningen beror på materialets kemiska bindningar. I dessa polära material är dipolerna slumpmässigt riktade så länge som det är utanför ett yttre fält. Med ett yttre fält linjeras dipolerna upp, vilket kan ge en stark reduktion av det yttre fältet. Vatten är ett exempel på ett polärt ämne. I väldigt höga yttre E-fält kan laddningsförskjutningen bli så stor att elektroner rycks loss från atomen (molekylen), materialet blir då joniserat och börjar fungera som en ledare. Detta är vad som exempelvis sker vid blixturladdningar under åskoväder. För varje material finns en sådan kritisk elektrisk fältstyrka där detta inträffar, det kallas för materialets genomslagshållfasthet och har enheten volt per meter (V/m).
Elektrisk polarisation (P)
Polarisationen i ett dielektriskt material definieras som mängden elektriska laddningsförskjutningar per volymsenhet.
Polarisationen P har enheten coulomb per kvadratmeter (C/m2) och utgör alltså summan av alla elektriska dipolmoment pi i en volym Δτ.
Elektrisk fältstyrka (E)
Varje laddning omger sig med ett elektriskt fält. Omkring flera laddningar blir det resulterande elektriska fältet lika med vektorsumman av bidraget från varje laddning. För N stycken laddningar blir det totala elektriska fältet E i en punkt lika med

Testladdning q i ett homogent e-fält E.
Placerar man i detta fält en testladdning q vars eget elektriska fält är försumbart, kommer den att påverkas av fältet med en bestämd kraft. Denna kraft är i varje punkt proportionell mot testladdningen. Proportionalitetskonstanten i detta förhållande utgör den elektriska fältstyrkan i punkten och betecknas med bokstaven E. Den elektriska fältstyrkan i en punkt definieras som kraften per (positiv) enhetsladdning i den punkten.
Då enheten för kraft är en newton (1 N) och enheten för laddning är en coulomb (1 C) kan enheten för elektrisk fältstyrka beskrivas som en newton per coulomb (1 N/C). Den kan även uttryckas som en volt per meter (1 V/m). I ett homogent elektriskt fält är styrkan och riktningen samma i alla punkter, t.ex. fältet i en plattkondensator, (bortsett från området närmast kondensatorns kanter).
Elektrisk susceptibilitet (Χe) och permittivitet (ε)
Elektrisk susceptibilitet Χe (av suscepti'bilis = mottaglig på latin) är ett dimensionslöst mått som anger hur känsligt ett material är för ett pålagt elektriskt fält, d.v.s hur mycket materialet polariseras då det utsätts för ett elektriskt fält. Detta i sin tur bestämmer permittiviteten hos materialet. Permittivitet är en fysikalisk storhet som beskriver hur ett elektriskt fält påverkar och påverkas av ett elektriskt isolerande material. Permittivitet betecknas med den grekiska bokstaven epsilon ε och har enheten en farad per meter (1 F/m). Hur polarisering P beror av ett materials susceptibilitet och permittivitet beskrivs genom uttrycket
P = ε0 Χe E
Den elektriska konstanten ε0 är permittiviteten för vakuum och kallas även för dielektricitetskonstanten ε0 = 8,85 pF/m. E är det elektriska fältet (V/m).
Susceptibiliteten Χe hos ett medium är relaterad till dess relativa permittivitet εr
Χe = εr - 1
i vakuum är εr = 1 och därför är susceptibiliteten Χe i vakuum lika med noll.
Χe = 0 I vakuum.
Elektrisk flödestäthet (D)
Den elektriska flödestätheten, även kallad den elektriska förskjutningen eller elektriska förskjutningsfältet, ger ett mått på tätheten av elektriska fältlinjer i förhållande till en viss area. Den elektriska flödestätheten är ett vektorfält som betecknas med D och har enheten en ampere-sekund per kvadratmeter (1 As/m2). Bokstaven D är vald från engelskans "displacement" (förskjutning), eftersom fältet är relaterat till fenomenet förskjutningsström i ett dielektrikum. Den elektriska flödestätheten är proportionell mot den elektriska fältstyrkan och det medium fältet befinner sig i.
D = ε0 E I vakuum. D = ε0 εr E I ett polariserbart medium.
ε0 är dielektricitetskonstanten för vakuum (ε0 = 8,85 pF/m), εr är den dimensionslösa relativa dielektricitetskonstanten för mediet mellan laddningarna, E är elektriska fältstyrkan (V/m).
Den elektriska flödestätheten D i en ideal plattkondensator motsvaras av den totala laddningen Q (C) fördelat över plattornas ytor A (m2).
Elektrisk kraft (F)
Mellan två laddade partiklar som befinner sig i varandras elektriska fält uppstår en elektrostatisk kraft. Olika laddningar attraheras till varandra, medan objekt med samma typ av nettoladdningar repellerar varandra. Denna kraftverkan mellan laddade partiklar i vila beskrivs med Coulombs lag,
där F är kraften i newton (N) och kallas för coulombkraften. q1 och q2 är laddningarna i coulomb (C), r är avståndet mellan laddningarna i meter (m), ε0 är dielektricitetskonstanten = 8,85 picofarad per meter (pF/m) och εr är den dimensionslösa relativa dielektricitetskonstanten för mediet mellan laddningarna.
Elektrisk potential (V)
Varje punkt i ett elektriskt fält kan tilldelas en elektrisk potential, vilken definieras som mängden arbete som åtgår för att förflytta en positiv enhetsladdning från en referenspunkt till den aktuella punkten. Referenspunkten har potentialen noll då den befinner sig på ett oändligt avstånd från det elektriska fältets källor. Vid beräkningar av elektriska kretsar brukar man använda jorden som referenspunkt. Den potentiella energin är då noll hos laddningar som är i kontakt med jorden. Den elektriska potentialen betecknas med V, och har enheten en volt (1 V).
Spänning (U)
Skillnaden i elektrisk potential mellan två punkter i ett elektriskt fält kallas elektrisk spänning eller potentialskillnad. Spänning betecknas med U och har enheten en volt (1 V). Spänningen blir positiv när den mäts mellan en punkt med högre potential till en punkt med lägre potential. Vanligtvis betecknas spänningens polaritet med ett plustecken i den punkt som har högst potential, och med ett minustecken i den punkt med lägre potential. Man kan även ange polariteten med en pil vars spets är riktad mot den lägre potentialen.
Ström (I)
En elektrisk ström I uppstår då elektriska laddningar förflyttas. Ström definieras som laddning per tidsenhet. De laddade partiklarna är vanligtvis elektroner, men kan även vara joner. För att få en ström i en ledare krävs det krafter från ett elektriskt fält som kan sätta fart på laddningsbärarna i ledaren. Den konventionella strömriktningen är den för en positiv laddning. Riktningen är från en högre (+) potential till en lägre (-), vilken motsvarar det pålagda elektriska fältets riktning. Strömmen är alltså positiv i fältets riktning. Enheten för elektrisk ström är en ampere (1 A). Ampere är en av de sju grundenheterna i SI-systemet. Man kan också uttrycka ampere som en coulomb per sekund, 1 A = 1 C/s. Elektrisk (likriktad) ström som passerar genom en tvärsnittsarea, t.ex. en metalltråd, fördelar sig jämnt över tvärsnittsytan. Därför kan strömtätheten definieras som ström per ytenhet. Strömtätheten är en vektorstorhet som betecknas med J och har enheten en ampere per kvadratmeter (1 A/m2). (SI = det internationella måttenhetssystemet).
Not. Läs mer om definitionen av SI-enheten en ampere i avsnittet "Magnetisk kraft" nedan.
Energi (W)
Elektrisk energi W är energi som representeras av coulombkrafter mellan elektriska laddningar. Mängden elektrisk energi i ett system definieras som det mekaniska arbete som tillförts för att flytta laddningarna från oändligt avstånd till det aktuella avståndet. Enheten för elektrisk energi är en joule (1 J), som är lika med en wattsekund, vanligtvis används en wattimme (1 Wh) eller en kilowattimme (1 kWh).
Effekt (P)
Effekt är mängden energi som omvandlas per tidsenhet. Effekt betecknas ofta med bokstaven P från engelskans power och kan bland annat yttra sig i form av ett värmeflöde eller arbete. Enheten för effekt är en watt (1 W). Ofta används en kilowatt (1 kW), som motsvarar 1000 W. Utöver watt finns det ett flertal enheter som betecknar effekt, exempelvis enheten hästkraft (hk). Enheten hästkraft är mer vanligt i Sverige än i övriga länder och används särskilt för att ange motoreffekter. I Sverige är 1 hk = 735,5 W och 1 kW = 1,36 hk.
Resistans (R)
Ledningselektronerna som förflyttar sig i en strömförande ledare erfar ett motstånd, jämförbart med friktion. Detta motstånd kallas resistans R och är proportionellt mot den elektriska fältstyrkan i ledaren. Resistans är alltså ett mått på strömbegränsningen hos en ledare eller komponent i en elektrisk krets. Ju högre resistansvärde en komponent har, desto högre spänning krävs det för att driva en ström med en viss styrka genom kretsen. Resistans mäts i ohm (Ω). I elektriska kretsar använder man sig av komponenter tillverkade av material med olika resistivitet (Ω m). Resistansen hos en ledare beror på: ledarens längd, tvärsnittsarea och materialets resistivitet. Resistiviteten är temperaturberoende, för en metallisk ledare ökar resistiviteten med temperaturen. Motsatsen (inversen) till resistans heter konduktans, som beskriver hur god ledningsförmåga en komponent har. Ett material som leder bra har hög konduktivitet.
Kapacitans (C)
Kapacitans beskriver förmågan att lagra elektrisk laddning, och betecknas med bokstaven C. Enheten för kapacitans är en farad (1 F) och definieras som en coulomb per volt, (1 C/V). Enheten en farad är stor, så stor att man tidigare ansåg kapacitanser på 1 F vara omöjliga att tillverka i rimlig storlek, men finns nu i komponenter inte större än några cm3. Vanligast är dock att man använder en microfarad 1 μF (10-6 F), en nanofarad 1 nF (10-9 F) och en picofarad 1 pF (10-12 F). För att lagra laddning används kondensatorer. Ett exempel är plattkondensatorn, vilken omnämnts tidigare, den består av två parallella metallplattor som isoleras från varandra med ett material emellan. Då man laddar plattorna med olika pontential skapas ett elektriskt fält och en spänning mellan dem. Kondensatortypens namn refererar ofta till distansmaterialet mellan plattorna. Materialet kallas dielektrikum och har stor betydelse för kondensators egenskaper och prestanda. Elektricitetsmängden, det vill säga den laddningsmängd Q (C) som kan lagras i kondensatorn, är proportionell mot den pålagda spänningen U (V) över kondensatorn enligt sambandet
Q = C U.
Kapacitansen C (F) i en kondensator bestäms, förutom av dess dielektrikum, också av plattornas area och avståndet mellan dem. Kondensatorer består inte alltid av två parallella plattor, utan finns även i andra former som t.ex. cylinderkondensatorer.
Om magnetism
Magnetism är ett fenomen med ett brett användningsområde och som har haft stor betydelse långt tillbaka i historien, särskilt inom sjöfarten. I Kina började man tidigt att använda magneter. Första gången som den magnetiska kraften omnämns i litteraturen var redan år 2637 f. Kr. i en beskrivning av en magnetkompass som den kinesiske kejsaren Hoang-ti hade. En kompass är i sin konstruktion mycket oansenlig, den består i princip bara av en nål som fritt kan rotera runt en pivot, centrerad i en graderad cirkel. Man ställer sig frågan: Hur kan ett så enkelt verktyg fungera som ett navigationsinstrument? Kortfattat kan man svara att då kompassnålen är tillverkad av ett magnetiskt järn ställer nålen in sig efter jordens magnetiska fält och pekar alltid i nord-sydlig riktning. Om man önskar ett mer fördjupat svar måste man redogöra för vad "magnetiskt järn" och "magnetiska fält" är, en sådan redogörelse försöker vi oss på i följande text.
Magnetism kan ytterst härledas till elektriska laddningar i rörelse. En ledare med konstant riktad ström omges av ett magnetiskt fält. Magnetiska fält finns också kring vissa material, som t.ex. järn, kobolt och nickel. Dessa materials magnetiska egenskaper har sitt ursprung i atomära elektronrörelser. I en (förenklad) atommodell kretsar negativa elektroner i en bana runt en positiv atomkärna. Man kan betrakta elektronens rörelse runt kärnan som en liten strömslinga. Varje elektron har dessutom ett s.k. spinn, en rotation kring sin egen axel. Detta spinn kan också betraktas som en strömslinga. Ofta har elektronerna motriktade omloppsbanor och spinnrörelser, varför nettorörelsen inte ger någon cirkulerande ström och därmed inga magnetiska effekter heller. I material med magnetiska egenskaper ger elektronernas spinn- och banrörelser kring kärnan upphov till s.k. magnetiska dipolmoment, vilka kan liknas vid atomära elementarmagneter.

En magnet har en sydpol och en nordpol, polerna ger upphov till ett magnetiskt fält. Mellan två magneter som befinner sig i varandras magnetfält uppstår en kraft vars riktning bestäms av polerna. Lika poler repellerar varandra och olika poler attraherar varandra. Här ser vi tydliga likheter med kraftverkan i elektriska fält. Tidigare är beskrivet hur elektriskt laddade partiklar utgör det elektriska fältets "källor". De elektriska laddningarna är så kallade elektriska monopoler, där fältlinjerna börjar eller slutar. Några monopoler för ett magnetiskt fält är ännu ej kända. En magnetisk pol kan aldrig isoleras. Om man halverar en magnet uppkommer nya poler och man erhåller två magneter med vardera en syd- och en nordpol. I magnetiska fält utgår fältlinjerna istället från de magnetiska dipolmomenten. I ferromagnetiska material (permanentmagneter) är dessa magnetiska dipolmoment konstant orienterade i en nord-sydlig riktning. I icke-magnetiska material, men som innehåller magnetiska dipolmoment, kan materialet magnetiseras genom influens av ett yttre magnetiskt fält. De magnetiska dipolmomenten ordnar sig då efter det yttre magnetfältets riktning, men så fort som det yttre fältet försvinner återgår materialet till sitt ursprungliga tillstånd. Det förekommer också material där en viss permanentmagnetism kvarstår, efter att materialet en gång har blivit magnetiserat.
Den här modellen, med atomära magnetiska dipolmoment, kan också tillämpas makroskopiskt, då man kan betrakta hela jordklotet som en dipol. Jordens magnetfält vid jordytan är (till 90 %) ett dipolfält. Kompassnålen, med sina mikroskopiska ferromagnetiska dipolmoment, påverkas av jordens magnetfält och nålen har därför en konstant nord-sydlig riktning.
Magnetiska storheter
Magnetiska dipolmoment (m)
Ett materials magnetiska egenskaper kan beskrivas med magnetiska dipolmoment m. Elektronernas spinn- och banrörelser kring en atomkärna kan liknas vid en liten strömslinga som ger upphov till ett magnetiskt dipolmoment. Atomerna är som små magnetnålar med nord- och sydändar, där m-vektorns spets är riktad från syd till nord. Magnetiska dipolmoment är vektorer med både storlek och riktning, enheten är en ampere kvadratmeter (1 Am2).
Magnetisering (M) och magnetiska fält
Magnetisering kan jämföras med polarisation inom elstatiken, magnetisering är ett mått på de magnetiska dipolmomentens förmåga att linjera upp sig i syd-nordlig riktning under påverkan av ett yttre magnetfält. De magnetiska dipolmomenten uppför sig olika för olika material, beroende på elektronernas spinn- och banrörelser kring atomkärnan. I de flesta material kommer elektronernas sammanlagda rörelser att motverka varandra och de magnetiska effekterna uteblir, men i ferromagneter kan de spontant samverka så att dipolmomentens vektorsumma blir skild från noll. Genom att betrakta de makroskopiska effekterna av denna samverkan i en volym Δτ kan man definiera magnetisering enligt
Magnetiseringen M är ett vektorfält som utgör den sammanlagda mängden magnetiska dipolmoment per volymsenhet och har enheten A m2/m3 = A/m, ampere per meter.
Magnetiska material och elektriska laddningar i rörelse ger upphov till magnetiska fält, vilka påverkar sin omgivning med magnetiska krafter. Ett magnetfält är ett vektorfält med storlek och riktning. En stavmagnet består av ett ferromagnetiskt material och omges av ett magnetfält. Dipolmomenten i järnmaterialet har en syd-nordlig riktning och fältlinjerna som utgår från magneten är riktade från stavens nordände till dess sydände. Fältstyrkan är proportionell mot linjetätheten. Magnetiska fält kan experimentellt synliggöras med hjälp av järnfilspån, vilka ställer in sig i fältlinjernas riktning.
Magnetiserande fältstyrka (H)
Den magnetiserande fältstyrkan H är primärt orsakad av fria strömmar (ström av elektriska laddningar) och är oberoende av mediet. Enheten är en ampere per meter (1 A/m). Magnetiserande fältstyrka är analog med den elektriska fältstyrkan E inom elstatiken och precis som denna är den magnetiserande fältstyrkan en vektoriserad storhet.
Magnetisk susceptibilitet (Χm) och permeabilitet (μ)
Magnetisk susceptibilitet Χm är en dimensionslös materialkonstant som beskriver hur mycket ett material magnetiseras i närvaro av ett H-fält. Vid magnetisering vrider sig de små atomära dipolmomenten parallellt med det pålagda fältet. Den magnetiska susceptibiliteten är ett mått på hur stor upplinjeringen blir för ett material. Följande definition beskriver magnetisk susceptibilitet
M = Χm H,
där M är magnetiseringen (A/m) och H är den magnetiserande fältstyrkan (A/m).
Ett materials magnetiska permeabilitet är dess förmåga att uppehålla skapandet av ett magnetiskt fält, m.a.o. graden av magnetisering som kvarstår efter att materialet har pålagts ett magnetfält. Permeabilitet brukar skrivas med den grekiska bokstaven μ. Enheten för permeabilitet är en henry per meter (1 H/m), eller en newton per ampere kvadrat (1 N/A2). Konstanten μ0 benämnes magnetiska konstanten, och är lika med permeabiliteten i vakuum. μ0 = 4π 10-7 H/m. För de flesta material skiljer sig permeabiliteten obetydligt från detta värde. Undantag utgör de ferromagnetiska materialen. Motsatsen till permeabilitet är reluktans.
Den magnetiska susceptibiliteten Χm hos ett medium är relaterad till dess relativa permeabilitet μr
Χm = μr - 1
i vakuum är μr = 1 och därför är den magnetiska susceptibiliteten Χm i vakuum lika med noll.
Χm = 0 I vakuum.
Magnetisk flödestäthet (B)
Magnetisk flödestäthet betecknas med bokstaven B och orsakas av både elektriska strömmar och magnetiserade material. Den magnetiska flödestätheten är alltså materialberoende.
B = μ0 μr H.
I uttrycket är μ0 den magnetiska konstanten, μr materialets permeabilitet och H den magnetiserande fältstyrkan. Magnetisk flödestäthet har enheten en tesla (1 T). En enhetsanalys visar att 1 T = 1 Wb/m2 = 1 Vs/m2 = 1 N/Am. Magnetisk flödestäthet mäts också i den mindre enheten 1 gauss = 10-4 Vs/m2. Det magnetiska fältet är liksom det elektriska fältet ett vektorfält. Flödestätheten har i varje punkt förutom storlek även riktning. Fältlinjerna utgår från en magnets nordände och går mot en magnets sydände. I ett magnetiskt fält kring en strömförande ledare kan fältriktningen beskrivas med "högerhandsregeln": Om man med höger hand griper om ledaren så att tummen pekar i strömmens riktning, pekar handens övriga fingrar i magnetfältets riktning.
Den magnetiska flödestätheten i en punkt utanför en lång rak strömförande ledare kan även beräknas med uttrycket
där B (T) är den magnetiska flödestätheten, μ är permaeabiliteten i materialet utanför ledaren, I (A) är den elektriska strömmen och a (m) är punktens avstånd till ledaren. Detta förhållande är en tillämpning av Ampères lag
(Ampères lag)
där dS är en oändligt liten sträcka (infinitesimal längd) i meter (m). ∮ är ett integraltecken som anger att man ska integrera längs en sluten kurva. Amperes lag kallas också cirkulationssatsen och används vanligtvis längs en kurva, där B är konstant. Men, satsen gäller även om man inte summerar längs flödeslinjerna.
För en tätt lindad solenoid som är lång i förhållande till sin diameter, är det magnetiska fältet inne i solenoidens mitt homogent och parallellt med solenoidens axel. Utanför solenoiden i närheten av mitten är fältet mycket svagt. Med Amperes lag kan följande uttryck för flödestätheten i en solenoid härledas
N är antalet lindningsvarv, l är solenoidens längd i meter (m). Storheten NI kallas för solenoidens amperevarvtal, och har förkortningen At med enheten en ampere (1 A). Storheten NI / l kallas solenoidens amperevarvtäthet och har enheten en ampere per meter (A/m).
Magnetisk kraft (F)
Den magnetiska kraft, som uppstår mellan två parallella strömförande ledare, är vinkelrät mot såväl den magnetiska flödestäthetens riktning som laddningarnas rörelseriktning. Om strömmarna är riktade åt samma håll, uppstår en kraft som attraherar de två ledarna till varandra. Om strömmarna istället är motriktade, kommer ledarna att repellera varandra. Kraften F på en laddning q som rör sig med hastigheten v i en magnetisk flödestäthet B kan skrivas
F = q(v x B)
där kraften F (N)är proportionell mot laddningen q (C) och kryssprodukten av hastigheten v (m/s) och flödestätheten B (T). Kraften är vinkelrät mot det plan, som bestäms av v och B. Tillämpar man högerhandsregeln skall högra handens tumme peka i strömmens rörelseriktning, pekfingret i flödestäthetens riktning och långfingret i kraftriktningen. Notera att högerhandsregeln gäller för strömmens och positiva laddningars rörelseriktning. För rörelseriktningen hos negativa laddningar (elektroner) kommer kraften att vara riktad åt det motsatta hållet, då man istället får använda vänsterhanden.
En rak strömförande ledare med längden l (m) som placeras vinkelrätt mot ett homogent magnetiskt fält med flödestätheten B (T) kommer att utsättas för en kraft F (N) som ges av
F = I (B x l)
och där I (A) är den elektriska strömmen.
Definitionen av SI-enheten en ampere
I SI-systemets definition av enheten för elektrisk ström med storleken en ampere har den magnetiska kraften betydelse som referens. Definitionen av en ampere lyder:
En ampere (1 A) är storleken av den konstanta elektriska ström som, då den genomflyter två parallella, raka ledare med oändlig längd och försumbart, cirkulärt tvärsnitt och placerade på ett avstånd av en meter från varandra i tomrum, åstadkommer mellan dessa ledare en kraft lika med 2×10-7 newton för varje meter ledare.
I definitionen för enheten en ampere ger strömmarna i de två ledarna upphov till ett magnetfält som skapar en kraft med storleken 2×10-7 N. Varför det är exakt detta värde kan härledas ur funktionerna för magnetisk flödestäthet samt magnetisk kraft
Avståndet a mellan ledarna är en meter och strömmarna I1 och I2 är symmetriska, med samma riktning och storleken en ampere. Den kraft F2 som påverkar längden l2 av ledaren två kan uttryckas med formeln
Storleken på den magnetiska kraften F2 beräknas genom att i uttrycket använda följande värden
I1 = I2 = 1 A
l2 = 1 m
a = 1 m
μ = μ0 = 4π 10-7 Vs/Am (permeabiliteten för vakuum)
som då ger
Magnetiskt flöde (Φm)
Det magnetiska flödet är proportionellt mot magnetfältets flödestäthet och en yta vinkelrät mot fältlinjerna. Enheten för magnetiskt flöde är en weber (1 Wb) som är lika med en voltsekund (1 Vs). I ett homogent magnetiskt fält är
Φm = B A
där B (Vs/m2) är lika med den magnetiska flödestätheten, och A (m2) är lika med arean vinkelrät mot fältlinjerna.
Magnetisk reluktans (Rm)
Magnetisk reluktans kan jämföras med elektrisk resistans och är ett mått på magnetiskt motstånd. Reluktans betecknas med Rm och enheten är 1 H-1. I likhet med hur det elektriska fältet får en elektrisk ström att följa en väg av minimal resistans, orsakar ett magnetiskt fält att ett magnetiskt flöde följer en väg av minsta magnetiska reluktans. Reluktansen Rm i en toroidkärna kan skrivas
där l = 2πR = flödeslinjernas medelväglängd genom järnet (R = toroidens medelradie). A = toroidens tvärsnittsarea. μr = materialets permeabilitet, och μ0 är den magnetiska konstanten, d.v.s permeabiliteten i vakuum.
Elektromagnetism
Kraftverkan i elektromagnetiska fält, lorentzkraften
En laddad partikel som rör sig i ett kombinerat elektriskt och magnetiskt fält, påverkas av krafter från båda dessa fält. De krafter Fe och Fm som en laddning q utsätts för när den förflyttas i elektriska respektive magnetiska fält ges av de två sambanden
Fe = E q elektriskt fält Fm = q(v x B) magnetiskt fält
där E är den elektriska fältstyrkan, v är laddningens hastighet och B är den magnetiska fältstyrkan. En kombination av dessa uttryck ger den resulterande kraften F, vilken kallas för lorentzkraften.
F = q(E + v x B) lorentzkraften
Den elektriska kraft Fe som påverkar en positiv laddning har samma riktning som det elektriska fältet har (lika med strömriktningen och motsatt elektronernas rörelseriktning). Den magnetiska kraften Fm är alltid vinkelrät mot det plan som definieras av en partikels rörelseriktning och den magnetiska flädesriktningen. Detta innebär att en laddad partikel som initialt har sin rörelseriktning från kraften i ett elektriskt fält, kommer att påverkas av den magnetiska kraften när partikeln kommer in i ett magnetfält. Eftersom den magnetiska kraften i varje punkt är vinkelrät mot en partikels rörelseriktning, kommer kraften på partikeln att skapa en rotationsrörelse. Magnetfältet uträttar därmed inte något arbete på partikeln. Ett statiskt magnetfält ändrar inte en partikels rörelseenergi, och hastigheten hos en laddad partikel som skjuts vinkelrätt in i ett homogent magnetfält kommer att vara konstant längs dess bana. Lorentzkraften utgår alltså en centripetalkraft. Partikeln rör sig först parallellt med E-fältet, inne i magnetfältet böjs den sedan av enligt högerhandsregeln för B-fält. Detta utnyttjas till exempel i tv-apparater med katodstrålerör för att avlänka elektronstrålar.
Halleffekt
En tunn metallplatta kan betraktas som en ledare. Om man skickar en ström genom plattan och placerar den vinkelrätt mot ett magnetfält kommer det att uppstå en spänning mellan två av plattans sidor. Denna spänning kallas hallspänning, UH. Ledningselektronerna antas ha drifthastigheten v vilken är riktad längs med ledaren. Med beteckningen B för magnetfältets flödestäthet erhåller man den magnetiska kraft Fm som de elektriska laddningarna qe påverkas av.
Fm = qe (v x B)
Kraftriktningen är vinkelrät mot det plan som definieras av partiklarnas rörelseriktning och den magnetiska flödestäthetens riktning. Ledningselektronerna kommer alltså att böja av mot ledarens kant, samtidigt som de fortsätter sin rörelse i ledarens längdriktning. Det blir ett överskott av elektroner i kanten av ledaren och motsvarande underskott i den andra kanten.
Denna laddningsfördelning ger upphov till ett elektriskt fält E mellan plattornas sidor och elektronerna kommer därför att samtidigt påverkas av kraften Fe från det elektriska fältet.
Fe = qe E
Den elektriska kraften har motsatt riktning än den magnetiska kraften. Ett jämviktstillstånd skapas där de båda krafterna Fm och Fe har samma storlek. Ledningselektronerna fortsätter sin rörelse i ledarens längdriktning och hallspänningen finns kvar så länge som ledaren utsätts för det magnetiska fältet.
Elektromagnetisk induktion, induktionsström och elektromotorisk spänning
Det magnetiska fältets kraftverkan på laddningar i rörelse är en fundamental egenskap med stor betydelse inom elläran. Halleffekten, som är beskriven i avsnittet ovan, är ett exempel på vad man kallar elektromagnetisk induktion, som är en direkt följd av magnetiska krafters påverkan på fria, rörliga laddningar. Den s.k. hallspänningen uppkommer då man låter en ström passera genom en tunn metallplatta placerad inuti ett magnetfält. Om man istället betraktar en hel ledare som förflyttas vinkelrätt mot fältlinjerna i ett magnetiskt fält, kommer de fria elektronerna i ledaren att påverkas av den magnetiska kraften
Fm = qe (v x B)
Kraften orsakar en laddningsförskjutning, så att ledarens ena del får ett överskott av elektroner, medan den andra delen får motsvarande underskott. Denna laddningsfördelning skapar en spänning mellan ledarens ändpunkter - en inducerad spänning.
Om ledarens ändar kopplas samman så att den utgör en sluten krets kommer det att flyta en ström i kretsen. Denna ström kallas induktionsström. Ledaren kan då jämföras med en spänningskälla. Den inducerade spänningen benämns ofta inducerad ems (elektromotorisk spänning). Induktionsströmmen, som den inducerade spänningen i en sluten krets ger upphov till, har alltid en sådan riktning att den motverkar orsaken till sin uppkomst (Lenz´ lag). Den inducerade spänningen betecknas med e och då vektorstorheterna hastigheten v, flödestätheten B och längden l är vinkelräta mot varandra kan den inducerade emsen beskrivas med
e = B v l (flödestäthet, hastighet och längd är vinkelräta mot varandra)
Induktionslagen
En inducerad spänning kan uppstå genom att en ledare eller ett magnetiskt flöde förflyttas i relation till varandra. Då ett magnetiskt flöde genom en sluten slinga ändras, induceras i slingan en spänning som bestäms av sambandet
(Faradays lag)
där e är momentanvärdet för den inducerade spänningen (ems) med enheten en volt (1 V), Φ är det magnetiska flödet med enheten en weber (1 Wb) som är lika med en voltsekund (1 Vs) och t är tiden i sekunder (s).
Förhållandet kallas Faradays lag, och denna induktionslag är grundläggande för hur bland annat transformatorer, elektriska motorer och elektriska generatorer kan konstrueras.
Sambandet ovan avser den inducerade spänningen i en trådslinga. Betraktar man istället en flat spole med N lindningsvarv, kan spolen anses bestå av N stycken seriekopplade slingor. När det magnetiska flödet genom en spole ändras, induceras i hela spolen en spänning som kan skrivas
Självinduktion och induktans (L)
Enligt Faradays lag uppstår en inducerad spänning i en spole (eller en slinga) om det magnetiska flödet genom spolen ändras. En flödesändring kan ske när det magnetiska flödet eller spolen förflyttas i förhållande till varandra, den kan även skapas då strömmen varierar. En ström i en spole genererar ett magnetfält, och genom att ändra riktning på strömmen genom spolen kommer även flödet att ändras, vilket ger upphov till en ems. Så länge som strömmen är konstant skapas ingen inducerad spänning, det är först då strömmen genom spolen ändras som emsen uppstår. Detta fenomen kallas självinduktion. Enligt Lenz´ lag skall den inducerade spänningen ha en sådan riktning att den motverkar orsaken till sin uppkomst. Den inducerade spänningen e motverkar ändringar i strömmen genom spolen, och kan skrivas
konstanten L kallas induktans eller självinduktionskoefficient. Enheten för induktans är en voltsekund per ampere (1 Vs/A), som är lika med en henry (1 H). L är en för spolen karakteristisk konstant. Den beror av spolens geometri och dess lindningstal. Hur dessa villkor bestämmer en spoles induktans ges av följande samband
där μ (H/m) är den magnetiska permeabiliteten i spolens material, N är antalet lindningsvarv, A (m2) är spolens tvärsnittsarea vinkelrätt mot fältlinjerna, l (m) är spolens längd.
En krets kommer att alstra ett magnetfält när en ström kopplas till den. Vid strömtillslaget induceras en spänning till följd av den magnetiska flödesändringen. Den inducerade spänningen söker motverka strömändringen. Denna egenskap vill man utnyttja och genom att ansluta en spole till kretsen kommer induktansen i spolen att skapa en större tröghet i kretsen. Vid varje strömändring kommer strömmen inte omedelbart att nå sitt slutvärde, utan först efter en kort tid intar den sitt stationära värde. En spole med stor induktans har betydelse för att förhindra strömrusning i en krets.
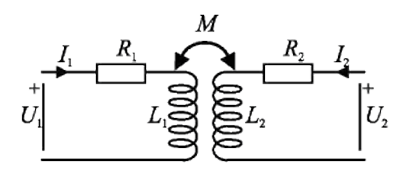
Ömsesidig induktans
Strömförande spolar som befinner sig i närheten av varandra påverkas av såväl sina egna som av varandras magnetfält. För att beräkna det magnetiska flödet genom en spole måste man således även inkludera summan av de delflöden som varje annan spole ger upphov till. Om man betraktar två spolar med strömmarna I1 och I2 kan man enligt superpositionsprincipen beräkna det magnetiska flödet Φ i varje spole.
Φ11 = k11i1 = det av i1 alstrade flödet genom varje varv av spole 1.
Φ12 = k12i1 = det av i1 alstrade flödet genom varje varv av spole 2.
Φ21 = k21i2 = det av i2 alstrade flödet genom varje varv av spole 1.
Φ22 = k22i2 = det av i2 alstrade flödet genom varje varv av spole 2.
Φ1 = Φ11 + Φ21 = det totala flödet genom spole 1.
Φ2 = Φ22 + Φ12 = det totala flödet genom spole 2.
Varje flödesbidrag är proportionellt mot den ström som alstrar bidraget. Konstanten k är en proportionalitetsfaktor som bestäms av spolarnas geometri och antal lindningsvarv, samt av spolarnas lägesförhållande till varandra.
Tidsberoende strömmar i spolarna skapar i takt varierande magnetflöden genom spolvarven och därmed induceras spänningar över spolarna. De inducerade spänningarna över spolarna 1 och 2 kan beskrivas med följande uttryck:
⇒
⇓
Ur dessa uttryck, av den inducerade spänningen i varje spole, erhåller man dels spolens självinduktans och dels en ömsesidig induktans.
L1 = N1 k11 = självinduktansen hos spole 1.
L2 = N2 k22 = självinduktansen hos spole 2.
M21 = N1 k21 = ömsesidiga induktansen hos spolarna 2 och 1.
M12 = N2 k12 = ömsesidiga induktansen hos spolarna 1 och 2.
Den ömsesidiga induktansen M21 är lika med den ömsesidiga induktansen M12.
M21 = M12
Om man låter det gemensamma värdet av M21 och M12 betecknas med bokstaven M kan man definiera spolarnas inducerade spänningar enligt
Elektriska komponenter
Resistorer
Resistorer, även kallade motstånd, används i elektriska kretsar för att skapa en resistans. Resistans är en elektrisk storhet som beskriver strömbegränsningen hos en ledare eller komponent i en elektrisk krets. Enheten för resistans är ohm (Ω). Enligt Ohms lag gäller att resistansen, R, utgör kvoten av spänningen, U, över en resistor och strömmen, I, genom den.
En komponents resistans bestäms av dess resistivitet, som är en materialegenskap med enheten ohm meter (Ωm). Alla material har en viss resistivitet, vars storlek varierar beroende på vilket ämne det är. Metaller har som bekant låg resistivitet, medan den är hög i keramiska material. Resistiviteten är också temperaturberoende, vilket innebär att resistiviteten hos en metallisk ledare ökar med stigande temperatur.
Resistorer har oftast fasta temperaturspecifika resistansvärden. En annan typ av resistorer är s.k. potentiometrar med resistansvärden som går att variera. Dessa ger en trimningsmöjlighet att reglera strömmen i kretsen, och kallas därför också för trimmotstånd eller trimpotetiometrar. I kretsschemor förekommer olika symboler för resistorer.

Resistansen hos en ledare beror på: ledarens längd, tvärsnittsarea och materialets resistivitet. En trådformig ledare med längden l (m), tvärsnittsarean A (m2) och resistiviteten ρ (Ωm) har resistansen:
Seriekopplade resistorer
Den totala resistansen i en krets med seriekopplade motstånd, där samma ström passerar genom alla, kan beräknas genom att addera samtliga resistanser enligt:
Rtot = R1 + R2 + R3
De seriekopplade motståndens totala resistans kan allmänt skrivas
Parallellkopplade resistorer
I en krets med parallellkopplade motstånd delar huvudströmmen I0 upp sig enligt Ohms lag på de olika resistanserna. Den totala resistansens inverterade värde blir då lika med summan av de ingående resistansernas inverterade värden.
Ett mer generellt uttryck för parallellkoppling av N stycken motstånd ges av
Kondensatorer
Kondensatorer och kapacitans
En kondensator är en passiv elektrisk komponent, som används i kretsar för att kortvarigt lagra laddning. En kondensator, typ en plattkondensator, utgörs av två metallplattor isolerade från varandra med ett dielektriskt material emellan. När metallplattorna ansluts till var sin pol på en spänningskälla uppstår en potentialskillnad och ett homogent elektriskt fält mellan dem. Fältstyrkan E är proportionell mot spänningen U och avståndet d mellan plattorna, enligt
För fältet kring en punktladdning gäller att fältstyrkan är proportionell mot laddningen. Detsamma gäller också för fältet mellan plattorna i detta fall. Följaktligen är elektricitetsmängden, det vill säga den laddningsmängd Q (C) som kan lagras i kondensatorn, proportionell mot den pålagda spänningen U (V) över kondensatorn. Följande samband råder
Q = C U.
Beteckningen C i uttrycket är kondensatorns kapacitans, och beskriver dess förmåga att magasinera laddning. Enheten för kapacitans är en farad (1 F), vilken definieras som en coulomb per volt, (1 C/V). Ju större kapacitans en kondensator har desto mer elektrisk laddning måste man tillföra för att nå en given spänning. Kapacitansen 1 F är vanligtvis för stor för praktiskt bruk. Ofta använder man kondensatorer i storleksordningen en microfarad 1 μF (10-6 F), en nanofarad 1 nF (10-9 F) och en picofarad 1 pF (10-12 F).
Kondensatortypens namn refererar ofta till distansmaterialet mellan plattorna. Det dielektriska materialet kallas dielektrikum och har stor betydelse för kondensators egenskaper och prestanda, exempelvis kan det bestå av keramik, plast, papper eller aluminiumoxid (denna typ kallas dock elektrolytkondensator).
Ytterligare en faktor som är avgörande för kapacitansstorleken är kondensatorns geometriska dimensioner. Med större metallplattor erhålls en högre kapacitans. En kondensator består inte alltid av två parallella plattor, den kan även ha andra former. Cylinderkondensatorer t.ex. består av två koncentriska metallcylindrar. Men, för enkelhets skull betraktar vi här en ideal plattkondensator. Kondensatorns totala laddning Q (C) fördelat över plattornas ytor A (m2) motsvarar den elektriska flödestätheten D.
Vidare förhåller sig den elektriska flödestätheten också till kondensatorns dielektrikum samt den elektriska fältstyrkan enligt följande samband:
D = ε0 E I vakuum. D = ε0 εr E I ett polariserbart medium.
ε0 är dielektricitetskonstanten för vakuum (ε0 = 8,85 pF/m), εr är den dimensionslösa relativa dielektricitetskonstanten för mediet mellan laddningarna, E är den elektriska fältstyrkan (V/m).
Utifrån dessa samband kan summeras att kapacitansen i en plattkondensator erhålls om man känner dess area, dielektrikum och distansen mellan plattorna:
Användning av kondensatorer
Kondensatorer används på många olika sätt främst inom växelströmstekniken. I elektriska svängningskretsar ingår alltid en kondensator, som t.ex i radiomottagare. Genom att kombinera kondensatorer och motstånd kan man skapa filter som blockerar vissa frekvenser. En vanlig tillämpning är kondensatorns egenskap att släppa igenom växelström, men inte likström. Detta utnyttjas för att likrikta växelström och i kopplingar där man vill skydda vissa delar mot likspänning, som de inte skulle tåla.
Kondensatorsymboler
I kopplingsschemor förekommer det olika kretssymboler för kapacitans. Vanligtvis ritas en kondensator som ett plattpar, oavsett hur den i praktiken är konstruerad.
Seriekopplade kondensatorer
När kondensatorer seriekopplas och ansluts till en spänningskälla kommer alla kondensatorer att laddas med en lika stor laddningsmängd, Q, eftersom laddströmmen är densamma i alla kondensatorerna.
Det inverterade värdet av ersättningskapacitansen Ctot till de tre seriekopplade kapacitanserna är lika med summan av delkapacitansernas inverterade värden:
Allmänt gäller för N stycken seriekopplade kapacitanser:
Parallellkopplade kondensatorer
I motsats till när man ansluter seriekopplade kondensatorer till en spänningskälla, kommer parallellkopplade kondensatorer att utsättas för en gemensam spänning med samma potentialskillnad över alla kapacitanserna.
Den laddningsmängd, Q, som varje kondensator laddas upp med blir då proportionell mot dess kapacitans och summan av alla delkapacitansernas laddning utgör den totala laddningsmängd som en tänkt ersättningskapacitans laddas med. Ersättningskapacitansen Ctot erhålls på följande sätt:
Ctot = C1 + C2 + C3
Allmänt gäller för N stycken parallellkopplade kapacitanser:
Upplagrad energi
Den upplagrade energin W i en kondensator med kapacitansen C och spänningen u är lika med
Denna energi kallas för elektrisk energi eftersom energin finns upplagrad i det elektriska fältet mellan kondensatorplattorna.
Spolar
 En spole är en passiv, induktiv komponent, även kallad induktor eller solenoid. Den kan liknas vid en metalltråd som är tätt ihoplindad i spiral, ibland kring en kärna av ett ferromagnetiskt material i form av en stav eller en ring, men även så kallade luftlindade spolar förekommer. Spolar används i kretsar bl.a. för att skapa induktans vid frekvensselektering. En spole som huvudsakligen används för att undertrycka växelspänningar kallas ofta för en drossel.
En spole är en passiv, induktiv komponent, även kallad induktor eller solenoid. Den kan liknas vid en metalltråd som är tätt ihoplindad i spiral, ibland kring en kärna av ett ferromagnetiskt material i form av en stav eller en ring, men även så kallade luftlindade spolar förekommer. Spolar används i kretsar bl.a. för att skapa induktans vid frekvensselektering. En spole som huvudsakligen används för att undertrycka växelspänningar kallas ofta för en drossel.
Kretssymbol
Som beteckning för induktans används bokstaven L och i kretsschemor ritas induktans med följande symbol:
Seriekopplade induktanser
Den totala induktansen som erhålls då spolar kopplas i serie motsvaras av summan av de olika seriekopplade spolarnas induktansvärden.
Parallellkopplade induktanser
I det fall då man har parallellkopplade induktanser utgörs den totala induktansen av summan för de parallekopplade spolarnas inverterade induktansvärden.
Induktans
En spoles induktans söker motverka alla förändringar hos den ström som passerar genom spolen. Induktans betecknas med bokstaven L och är en elektrisk storhet med enheten en voltsekund per ampere (1 Vs/A), som är lika med en henry (1 H). När en elektrisk ström går genom en ledning skapas det kring ledaren ett magnetiskt fält. Kvoten mellan det av strömmen alstrade magnetfältets flöde Φ (Vs) och strömstyrkan i (A) utgör spolens induktans
Enligt Faradays lag uppstår en inducerad spänning ems om det magnetiska flödet genom spolen eller slingan ändras. Den inducerade spänningen brukar betecknas med bokstaven e och har enheten en volt (1 V).
(Faradays lag)
En ändring av det magnetiska fältets flöde kan ske genom att strömmen i spolen ändras. Så länge som strömmen är konstant sker ingen flödesändring och då uppkommer inte heller någon ems. Det är först vid en strömändring som en spänning induceras. Fenomenet kallas för självinduktion. Enligt Lenz' lag ska den inducerade spänningen ha en sådan riktning att den motverkar orsaken till sin uppkomst. Om strömmen genom spolen ökar, söker den inducerade spänningen att motverka ökningen. Och vice versa, minskar strömmen, söker emsen att öka den. Det är själva strömändringen som den inducerade spänningen söker motverka. Ett annat samband för inducerad spänning ges av
Induktansen L är för en spole en karakteristisk konstant, även kallad självinduktionskoefficient. Den beror av spolens material, geometri och dess lindningstal enligt
där μ (H/m) är den magnetiska permeabiliteten i spolens material, N är antalet lindningsvarv, A (m2) är spolens tvärsnittsarea vinkelrätt mot fältlinjerna, l (m) är spolens längd.
Upplagrad energi i induktans
Den upplagrade energin W i en induktans L med strömmen i är lika med
Denna energi kallas för magnetisk energi eftersom energin finns upplagrad i magnetfältet som finns inuti och runt spolen.
Spolens impedans
Spolar har, förutom ett likspänningsmotstånd som utgörs av själva tråden, också ett frekvensberoende motstånd kallat reaktans. Den induktiva reaktansen XL har enheten en ohm (1 Ω) och beräknas ur formeln
XL = ω L
där ω är vinkelhastigheten (rad/s) som är lika med 2·π·f, där f är frekvensen (Hz).
Spolens reaktans och resistans ger tillsammans dess impedans som brukar betecknas med bokstaven Z.
ZL = √(XL2 + R2)
Spolens ekvivalenta schema

För att lättare förstå hur en spole fungerar som komponent, kan man beskriva den med ett förenklat ekvivalent schema.
I figuren är beteckningarna L = induktansen, RS = serieresistansen och CL = egenkapacitansen i spolen, t.ex. kapacitans mellan trådvarv (kallas även läck-, parasit-, eller strökapacitans).
Q-värdet (Q för engelskans quality), eller spolens godhetstal, är kvoten mellan spolens reaktans och dess serieresistans. Lägre resistans ger högre Q-värde och brantare filter.
Q = XL / RS
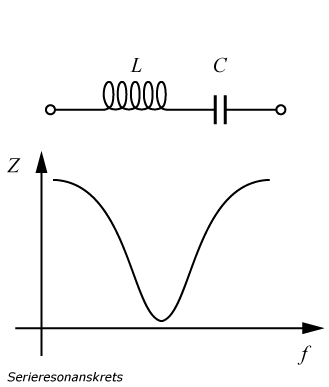
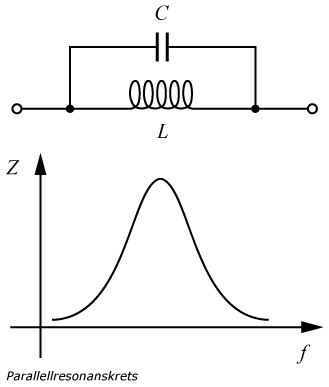
Resonans
En spole tillsammans med en kondensator bildar en svängningskrets. Denna krets har en resonansfrekvens, d.v.s. en frekvens där reaktansen hos spolen och kondensatorn är lika stora. Vid denna frekvens är den sammanlagda impedansen som lägst om de är seriekopplade, och som högst om de är parallellkopplade. Resonansfrekvensen f (Hz) erhålls ur sambandet
f = 1 / (2π · √(LC))
Egenkapacitansen CL i spolen bildar en svängningskrets med induktansen. Dess resonansfrekvens kallas självresonansfrekvens (SRF). Egenkapacitansen kan ställa till problem vid höga frekvenser om man inte tar den i beaktande. Testfrekvensen för Q-värde bör vara högst en tiondel av självresonansfrekvensen.
Ideal transformator
En transformator består i princip av två spolar, som är lindade på samma järnkärna. Spolarna är elektriskt isolerade från varandra. En växelström som påförs den ena spolen orsakar ett varierat magnetiskt flöde i järnkärnan. Detta flöde passerar även genom den andra spolen och enligt induktionslagen kommer en varierad spänning att induceras. Det sker alltså en energiöverföring från den ena spolen (lindningen) till den andra via flödet i järnkärnan. Den lindning (spole) som tillförs energi kallas primärlindning, och den lindning som levererar energi kallas sekundärlindning.
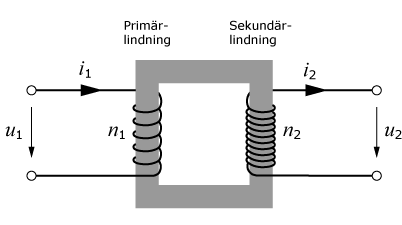 Transformatorkärna med primär- och sekundärlindning |
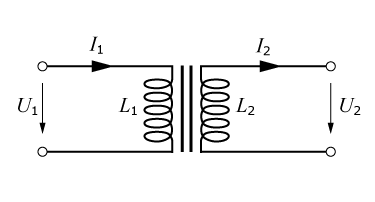 Symbol för transformator |
 |
 |
Transformatorer är en tillämpning av vad man kallar "kopplade magnetiska kretsar". Med en ideal transformator menas en magnetisk koppling som är fullständig, vilket innebär att det totala magnetiska flöde som genereras av primärlindningen också passerar genom sekundärlindningen, d.v.s. det finns inget läckfält.
En ideal transformator har:
I praktiken existerar det inte någon "ideal transformator", men genom att använda laminerade järnkärnor förbättras egenskaperna och man kommer närmare en ideal transformator. Laminerade järnkärnor är uppbyggda av metallplåtar i mjukjärn som fogats ihop till ringformade kärnor. Vid höga frekvenser används ferritkärnor bestående av sammanpressat pulver från ferromagnetiska material.
För att beskriva det samband som gäller vid energiöverföringen mellan en transformators primärlindning och dess sekundärlindning görs antagandet att transformatorn är av typen ideal. Växelströmmen på primärlindningen ger upphov till ett variabelt magnetiskt flöde i järnkärnan. Det varierande flödet skapar enligt induktionslagen en inducerad spänning, vilken erhålls i såväl primär- som sekundärlindningarna. De spänningar som induceras är proportionella mot antalet lindningar. Uttrycket för induktionslagen är kallat Faradays lag, där e är lika med den inducerade spänningen, Φ är det magnetiska flödet och t är tiden. Antalet varv på primärlindningen är N1 varv och sekundärlindningen har N2 varv.
Om sekundärkretsen är öppen (tomgång), gäller sambanden
e1 - u1 = 0 e2 - u2 = 0
Relationen mellan den tillförda spänningen u1 och spänningen u2 ut från transformatorn, är således ett linjärt förhållande som utgörs av kvoten mellan antalet varv på primärlindningen och antalet varv på sekundärlindningen.
Samma förhållande gäller även för växelspänningarnas effektivvärden U1 och U2.
Denna kvot mellan effektivvärdena U1 och U2 kallas för transformatorns omsättningstal.
Halvledare
Halvledartekniken har sedan andra halvan av 1900-talet, efter uppfinningen av transistorn 1947, haft en enorm utveckling. Halvledare förekommer i stort sett i all modern elektronik. Exempel på halvledarkomponenter är: termistorer, dioder, transistorer, likriktare, förstärkare, microprocessorer m.fl.
Halvledarmaterial har den egenskapen att de varken kan betecknas som ledare eller isolatorer. Halvledare är fyrvärda ämnen, såsom kisel (Si) och germanium (Ge), med fria elektroner och hål. Dessa material kan man radikalt förändra ledningsförmågan hos genom s.k. dopning, då man tillsätter ytterst små mängder tre- eller femvärda ämnen (störämnen). Jämvikten mellan elektroner och hål kommer då i obalans.
Om man dopar kisel med bor (B), som är ett trevärt störämne, kommer det dopade området i kristallen att få fler hål än antal fria elektroner. Ett sådant material kallas p-dopat eftersom hålen har har positiv laddning. Om man istället tillsätter arsenik (As), vilket är ett femvärt störämne, kommer det dopade materialet att ha fler fria elektroner än antal hål. Kristallen blir då n-dopad. I en p-dopad kristall är alltså flertalet fria laddningsbärare positiva och i en n-dopad kristall är de negativa. Hålen i det p-dopade materialet definieras som majoritetsbärare och elektronerna som minoritetsbärare. I den n-dopade kristallen är det tvärtom, där är elektronerna majoritetsbärare och hålen minoritetsbärare. Notera att oavsett vilken typ av dopning som används, är dock halvledarkristallen i sin helhet elektriskt neutral.
pn-övergång
Om en del av en halvledare p-dopas och den andra delen n-dopas erhåller man en pn-övergång i gränsytan mellan dessa två områden. Inom halvledartekniken spelar denna pn-övergång en central roll.
För att beskriva hur en pn-övergång fungerar kan man betrakta en halvledare som har ett p-dopat skikt och ett n-dopat skikt. Halvledarens grundmaterial är kisel. I n-skiktet är kislet dopat med ett ämne som har fem valenselektroner, exempelvis fosfor (P), och i p-skiktet har dopämnet tre valenselektroner, t.ex. bor. Det resulterar i att n-skiktet får ett överskott av elektroner, medan det i p-skiktet kommer att fattas elektroner. Elektronkoncentrationerna är alltså olika på ömse sidor om kontaktskiktet. Mellan p- och n-skikten skapas det en övergång, där elektroner och hål kan diffundera emellan. De femvärdiga störatomerna kallas för donatoratomer, eftersom de avger en fri elektron till kristallen och de trevärda atomerna, som har brist på elektroner, kallas för acceptoratomer. Donatoratomerna blir positivt laddade när de fria elektronerna lämnar atomen, och acceptoratomerna blir negatitivt laddade när de tar emot elektroner. Gränsskiktet mellan p- och n-materialen kommer att tömmas på fria laddningar. Detta område kallas därför för utarmningsområde.

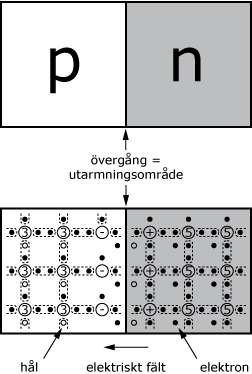
Utarmningsområdet
I det n-dopade skiktet definieras elektronerna som majoritetsbärare och hålen som minoritetsbärare. I det p-dopade skiktet är det tvärtom, där är hålen majoritetsbärare och elektronerna minoritetsbärare. När majoritetsbärarna diffunderar över pn-övergången kommer n-skiktet att få en positiv laddningsfördelning och p-skiktet blir övervägande negativt. Det byggs upp ett elektriskt fält som är riktat från n- till p-skikt. Efterhand får majoritetsbärarna det allt svårare att ta sig över pn-övergången och till slut är det uppkomna elektriska fältet så kraftigt att ett jämviktstillstånd inträder och fältstyrkans ökning avstannar. Vid pn-övergången bildas det en potentialbarriär i storleksordningen några tiondels volt (typiskt värde är 0,5 till 0,7 V). Här möter majoritetsbärarna ett motstånd, men minoritetsbärarna däremot får det lättare att diffundera över pn-övergången.
Om en spänning kopplas till pn-övergången med minus till p-skiktet och plus till n-skiktet, kommer potentialbarriärens nivå att öka och det blir ännu svårare för hål från p-sidan att ta sig över till n-sidan, och tvärtom för elektroner från n-sidan att ta sig över till p-sidan. Det resulterar i att ingen ström flyter. (Dock går det en liten ström av minoritetsbärare på grund av termiskt alstrade elektron-hålpar i hela kristallen). Med en spänning som kopplas till pn-övergången på detta sätt, sägs pn-övergången vara förspänd i backriktningen.
Om spänningen istället kopplas med pluspolen till kristallens p-skikt och minus till n-skiktet, kommer potentialbarriären att minska. Fria laddningsbärare får då lättare att diffundera över pn-övergången och en ström kan passera den. Pn-övergången är i detta fall förspänd i framriktningen.
En enda pn-övergång kan användas som en diod, genom att den släpper fram ström i en riktning. Med två pn-övergångar kan man konstruera en transistor.


Termistorer
Halvledare är känsliga för temperaturförändringar. Materialets ledningsförmåga är direkt proportionell mot antalet fria laddningsbärare. När temperaturen ändras påverkas atomstrukturen i halvledarmaterialet, de s.k. kovalenta bindningarna bryts upp och nya elektron-hålpar bildas, vilket medför en ändring i ledningsförmågan. En halvledare där man nyttjar denna temperaturkänsliga egenskap hos materialets ledningsförmåga, kallas för en termistor. Eftersom kisel och germanium är alltför känsliga för föroreningar, så används istället metalloxider såsom nickeloxid (NiO), manganoxid (Mn2O3) m.fl.
Termistorer används som temperaturgivare i t.ex. temperaturregleringskretsar, men även i andra sammanhang som t.ex. för att mäta effekt hos laserljus eller mikrovågor från en mikrovågssändare. Laserljuset resp. mikrovågorna värmer upp termistorn och genom att mäta ändringen i ledningsförmågan får man ett mått på effekten hos det elektromagnetiska fältet.
Ledningsförmågan i en termistor ökar med stigande temperatur, d.v.s. halvledarmaterialet har en negativ temperaturkoefficient (NTC-motstånd). Det är tvärtemot vad gäller för en metall, där ledningsförmågan minskar med stigande temperatur, d.v.s. metall har en positiv temperaturkoefficient (PTC-motstånd).
Dioder
Dioder kan användas för att släppa fram elektrisk ström i endast en riktning. Namnet kommer av att den har två elektroder, anod och katod. Dioden uppfanns redan på 1870-talet. Rördiodens principer blev kända 1873 och ett år senare kom kristalldioden. De kallades i början för likriktare. Kristalldioder och elektronrör användes bl.a. i tidiga radiomottagare. Numera är det vanligast att dioder består av halvledare. Dioder förekommer i många olika varianter för olika användningsområden, t.ex. zenerdiod, schottkydiod, lysdiod, fotodiod, kapacitansdiod, tunneldiod m.fl.
En vanlig halvledardiod utgörs av en halvledare i kisel, som i ena änden är p-dopad och i andra änden n-dopad. Skiktet mellan det p-dopade och det n-dopade området kallas för en pn-övergång. Dioder gjorda av dopat kisel börjar leda ström i framriktningen när spänningen över elektroderna överstiger ungefär 0,65 volt. Denna spänning kallas diodens framspänningsfall. En äldre typ, germanium-dioden har ett lägre framspänningsfall, vilket kan vara användbart i vissa tillämpningar. Ett annat material som används är galliumarsenid som används i lysdioder och för dioder som ska fungera vid mycket höga frekvenser.
Likriktardioden
I avsnittet med rubriken "Halvledare" beskrivs hur en pn-övergång i en halvledare kan fungera som en diod. Sambandet mellan ström och spänning över en pn-övergång kan skrivas på följande sätt:
I = I0 (e(qU / pkT) - 1)
där I0 är backströmmen genom pn-övergången, p är en materialkonstant som är 1 för Ge och 2 för Si, q är elektronladdningen, k är Boltzmanns konstant, T är temperaturen i °K, U är spänningen som räknas positiv i framriktningen.
Diodens I/U-karakteristik är illustrerad grafiskt i nedanstående figur:
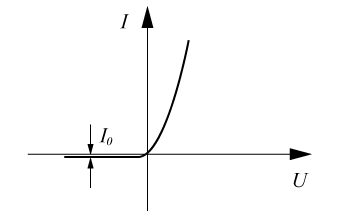
I diodekvationen har man inte tagit hänsyn till storleken hos halvledarmaterialets bandgap, som ger en spänningströskel för framspänningen hos pn-övergången. För germanium är tröskelspänningen ca 0,2 V, medan den för kisel är ca 0,6 V. Vid likriktning av små växelströmskretsar med halvledardioder i kisel, är det därför viktigt att ta hänsyn till detta framspänningsfall. Kisel har däremot en avsevärd fördel vad gäller backströmmen I0 i jämförelse med backströmmen för germanium som är av storleksordningen mikroampere (μA), för kisel är backströmmen tusen gånger mindre, i storleksordningen nanoampere (nA).
Liksom strömmen I genom pn-övergången är temperaturberoende, är även backströmmen I0 temperaturkänslig. För både kisel och germanium gäller att backströmmen fördubblas varje gång som temperaturen ökar med 10 °C.
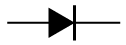
Symbolen för en likriktardiod har en pil som motsvarar diodens framriktning, i bilden nedan är den från vänster till höger.
Zenerdioden
Vid en tillräckligt hög negativ spänning sker ett genombrott då strömmen ökar lavinartat. Dioder som konstruerats för att användas just i genombrottsområdet kallas zenerdioder. Det krävs en fältstyrka på ca 107 - 108 V/m. Det är då som det elektriska fältet är så pass starkt att en bunden elektron kan bryta sig loss från sin kovalenta bindning. Detta kallas zenereffekt. Vid högre fältstyrkor bidrar ett annat fenomen till genombrottet, som då kallas lavineffekt. Denna orsakas av att termiskt genererade laddningsbärare får så stor kinetisk energi av det elektriska fältet att de vid kollision med gitteratomer kan bryta upp kovalenta bindningar och på så vis skapa nya laddningsbärare, som i sin tur får så stor energi att även de kommer att alstra nya laddningsbärare o.s.v.
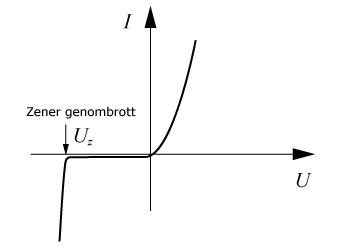
Det förekommer två olika sorters symboler för att beteckna en zenerdiod:
Temperaturberoendet hos en zenerdiod brukar anges som den procentuella ändringen av zenerspänningen per grad och ligger normalt inom området ± 0,1 % / °C. En zenerdiod kan användas för att stabilisera en likspänning, som spänningsreferens eller som spänningsskydd.
Kapacitansdioden
Kapacitansdioden, eller varaktordioden, fungerar som en spänningsstyrd kapacitans. Ju lägre spänningen är, desto högre blir kapacitansen. Denna egenskap förekommer också i en vanlig backspänd diod, men är optimerad i kapacitansdioder. Tjockleken hos utarmningslagret hos en pn-övergång beror av backspänningens storlek. Med ökad backspänning växer utarmningslagret, vilket resulterar i att de ledande områdena i pn-övergången flyttas längre isär. Detta medför att pn-övergången uppträder som en kapacitans som kommer att minska med ökande backspänning. Kapacitansens storlek bestäms av sambandet:
där C är kapacitansen, U är backspänningen och m är en konstant som beror på hur övergången från p- till n-skikt sker. Vid abrupt övergång är m = ½. Sker övergången istället gradvis kommer m att anta andra värden.
Symbolen för en kapacitansdiod:
Transistorer
Transistorer tillverkas numera uteslutande i halvledarmaterial. De används till signalmodulering och som signalförstärkare, strömbrytare, spänningsreglerare m.m. En transistor kan liknas vid en justerbar "strömventil" som styr en utsignal baserat på en insignal. Transistorer tillverkas som diskreta komponenter eller som delar av integrerade kretsar. De utgör en nyckelkomponent inom modern elektronik. I digitala kretsar verkar flera sammankopplade transistorer som snabba omkopplare och bildar tillsammans nätverksstrukturer för logiska grindar och mikroprocessorer. I analoga kretsar används transistorer som förstärkare, samt till många andra funktioner som byggs upp tillsammans med passiva komponenter. Transistorer finns i många varianter, de delas in i två huvudtyper: bipolära transistorer baserade på pn-övergångar, samt unipolära fälteffekttransistorer med undergrupperna utarmningstyp och anrikningstyp.
Bipolära transistorer
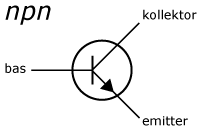
En bipolär transistor är en halvledare som har dopats så att den innehåller två stycken pn-övergångar. Det förekommer två typer: pnp, som har ett n-skikt mellan två p-skikt, och npn, med ett p-skikt mellan två n-skikt.
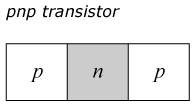
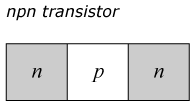
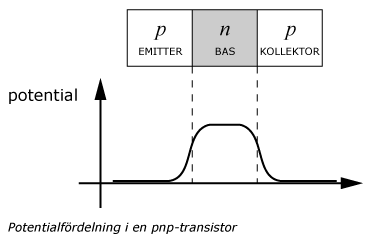
De tre skikten kallas för emitter, bas och kollektor. Emitter och kollektor har samma typ av dopning, medan basen har motsatt typ. Dopningsgraden, d.v.s. koncentrationen av störatomer, är oftast mycket lägre i basen än vad den är i de övriga två skikten, emitter och kollektor. Vid båda pn-övergångarna kommer en potentialbarriär att byggas upp. För en pnp-transistor kommer potentialfördelningen att bli som visas i figuren nedan.
En transistor kan ha fyra s.k. arbetslägen: strypt, aktiv, inverterat aktiv och mättad. Vilken typ av arbetsläge som transistorn har beror på hur den spänningssätts, om de två pn-övergångarna är i fram- eller backriktning.
Aktivt arbetsläge
Om man ansluter två yttre spänningar till en pnp-transistor, med den ena spänningen kopplad mellan emitter och bas, och den andra spänningen mellan emitter och kollektor, och där båda spänningskällornas pluspoler går till emittern enligt figuren nedan, kallas det för en GE-koppling (gemensam emitter). Pn-övergången mellan bas och emitter är i detta fall framspänd och bas-kollektordioden är backspänd. Den här typen av koppling är transistorns normala, aktiva arbetsläge. I detta läge kan transistorn fungera som en förstärkare, där kollektorströmmen beror av basströmmen.
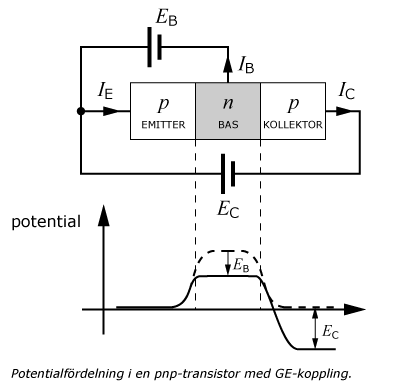
Strömförstärkningen i en pnp-transistor med GE-koppling förklaras med att då spänningarna ansluts och spänningen EB överstiger 0,65-0,7 V, kommer potentialbarriären mellan bas och emitter att minska och potentialen i kollektorområdet kommer att bli negativ i förhållande till emittern. Då potentialbarriären mellan bas-emitter minskas kan hål lättare passera från emittern till basen. Om basen har låg koncentration av störatomer och dess tjocklek är liten, är sannolikheten för rekombination liten. Merparten av hålen kommer då att fortsätta till kollektorn, eftersom den backspända bas-kollektordioden inte motverkar hålens rörelse. En relativt liten ändring av spänningen EB och därmed basströmmen IB medför en stor ändring av kollektorströmmen IC. Följande samband gäller:
IC = β · IB
där β är transistorns strömförstärkningsfaktor. Strömförstärkningsfaktorn kan variera kraftigt, mellan 20 till 1000 ggr. Den är också starkt temperaturberoende.
Storleken på den ström som passerar från emitter till kollektor bestäms av hur stor basströmmen IB är, som i sin tur beror på den pålagda spänningen EB. Om EB är liten, kommer potentialbarriärens minskning att vara liten och bara en liten ström kan passera. Om däremot EB är stor, kommer potentialbarriären att minska mycket vilket resulterar i att en stor kollektorström kan passera.
Basströmmen IB är relativt mycket liten, i storleksordningen mikroampere, medan emitterströmmen IE oftast är i milliampereområdet. Strömmarna IE och IC kan då antas vara lika stora.
IE = IC + IB,
då IB är mycket liten kan man skriva:
IE ≈ IC
Inverterat aktivt läge
Om man växlar fältriktningen i det aktiva läget, så att bas-emitterdioden blir backspänd och bas-kollektorn blir framspänd, sägs transistorn vara i inverterat aktivt läge. Strömmen genom emittern (som nu tagit rollen som kollektorn tidigare hade) förhåller sig till basströmmen enligt följande:
IE = βR · IB
Den inverterade strömförstärkningsfaktorn βR är i regel mycket mindre är den ordinarie strömförstärkningsfaktorn β, varför transistorn är en dålig förstärkare i inverterat läge. Däremot är spänningen EC mycket mindre än ens det mättade lägets EC sat så låga värden som några millivolt kan förekomma. Detta gör transistorn till en utmärkt strömbrytare i inverterat läge, och används i denna konfiguration i TTL-logik.
Strypt arbetsläge
När transistorns båda pn-övergångar är backspända, d.v.s. spänningen mellan bas och emitter är mycket lägre än 0,6 V, beter sig transistorn som en backspänd diod. Förutom en oftast obetydlig läckström på några nanoampere, passerar det då nästan ingen ström mellan bas och emitter eller kollektor och emitter. I detta läge sägs transistorn vara strypt.
Mättat läge
När båda pn-övergångarna är framspända befinner sig transistorn i ett mättat eller bottnat läge. Transistorn fungerar då som en sluten strömbrytare, och mycket ström kan flöda genom kollektorn och emittern. Ett spänningsfall mellan dessa två områden finns dock kvar, EC sat = 0,2 V (sat från engelska saturation = "mättnad").
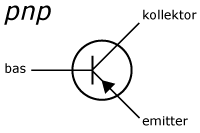
Symboler
Emitter-, bas- och kollektorströmmarna, IE, IB och IC brukar betecknas som positiva när strömmen går in mot transistorn. För en pnp-transistor i aktivt arbetsläge kommerIB och IC att vara negativa. Strömriktningen då transistorn är kopplad i aktivt läge ingår i symbolerna för bipolära pnp- och npn-transistorer.
Transistorers karakteristik
En transistors karakteristik framgår av de diagram som brukar finnas i fabrikanternas datablad. På transistorns "ingångssida" finns bas-emitterdioden. Sambandet mellan EB och IB följer en vanlig diodkurva och kallas ibland för transistorns ingångsdiagram. Transistorns "utgångssida" utgörs av det som finns mellan kollektor och emitteranslutningarna. Studerar man kollektordiagrammet, eller som det ibland kallas för utgångsdiagrammet, finner man att sambandet mellan EC och IC är extremt olinjärt. Kollektorströmmen IC är i det närmaste oberoende av kollektor-emitterspänningen EC. Istället är det basströmmen IB som styr kollektorströmmen, och basströmmen har därför införts som en parameter. Grovt kan man säga att kollektorströmmen är proportionell mot basströmmen.
Fälteffekttransistorer
 Fälteffekttransistorer (förkortas FET) är spänningsstyrda transistorer, till skillnad från de bipolära transistorerna som ju är strömstyrda. Man brukar urskilja två typer av fälteffekttransistorer, de av spärrskiktstyper som kallas JFET (junction field effect transistor) eller helt enkelt FET, och dessutom finns det en typ av fälteffekttransistorer med isolerad styrelektrod som kallas MOSFET-transistorer (metal oxide semiconductor field effect transistor).
Fälteffekttransistorer (förkortas FET) är spänningsstyrda transistorer, till skillnad från de bipolära transistorerna som ju är strömstyrda. Man brukar urskilja två typer av fälteffekttransistorer, de av spärrskiktstyper som kallas JFET (junction field effect transistor) eller helt enkelt FET, och dessutom finns det en typ av fälteffekttransistorer med isolerad styrelektrod som kallas MOSFET-transistorer (metal oxide semiconductor field effect transistor).
JFET
En JFET-transistor består av ett n-dopat material försett med två elektroder som kallas "source" = S och "drain" = D. Det är engelska benämningar som avspeglar elektrodernas funktioner, svenska termer kan även vara: "källa" och "utlopp". I source avges fria laddningsbärare som tas emot i drain. Fälteffekttransistorn har också två kraftigt p-dopade områden, som kallas för "gate" = G, på svenska även grind eller styre. Genom att man lägger en elektrisk spänning, s.k. styrspänning, på den isolerade elektroden "gaten" kan elektrisk ström passera mellan elektroderna drain och source, och därigenom skapas ett elektriskt fält. Det elektriska fältet styr i sin tur bredden på den kanal i vilken laddningarna kommer att förflyttas.
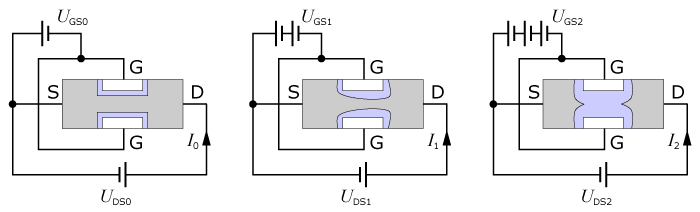 I figurerna är:
I figurerna är:
UGS0 < UGS1 < UGS2 I0 > I1 I2 = 0
Om en negativ spänning kopplas till gate-elektroden medför det att pn-övergången blir backspänd och att området i närheten av pn-skiktet töms på fria laddningsbärare. Ju lägre spänningen på gaten är desto större blir utarmningsområdet och desto svårare får strömmen att ta sig från S till D. En liten spänningsändring på gate-elektroden resulterar i en kraftig variation av strömmen genom transistorn. Vid en tillräckligt stor negativ gatespänning kommer strömmen att strypas helt. En FET kan därför användas som strömbrytare i en krets.
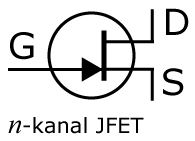
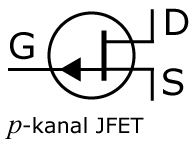
Symboler
Nedan visas symbolerna för en JFET-transistor typ n-kanal respektive p-kanal.
MOSFET
I en MOS-transistor är styrelektroden isolerad från kanalen med ett oxidskikt, vilket ger en ännu högre ingångsresistans än hos en JFET. MOS-transistorer finns i två typer: utarmningstyp och anrikningstyp.
Utarmningstyp
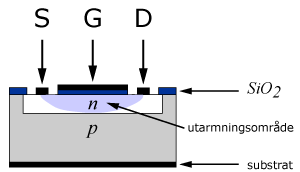
I figuren här intill visas en principskiss av hur en MOS-transistor av utarmningstyp är uppbyggd. Source S och drain D utgörs av två kraftigt n-dopade områden i en p-dopad kiselplatta. Mellan S och D är en svagare dopad n-kanal. Oxiden mellan styrelektroden och n-kanalen utgörs ofta av kiseldioxid (SiO2). Styrelektroden och n-kanalen kan betraktas som en kondensator med kiseldioxiden som dielektrikum.
Om en negativ spänning ansluts till styrelektroden kommer en positiv laddning att induceras i n-kanalen och ett utarmningsområde bildas. Storleken på utarmningsområdet beror av storleken på spänningen som läggs på styrelektroden. Även positiva spänningar kan kopplas till styrelektroden på grund av oxidskiktet i motsats till en styrspänningen till en JFET, där den alltid måste ha samma polaritet. Strömmen genom transistorn styrs då på motsvarande sätt som för en JFET av spänningen på styrelektroden.
Symboler
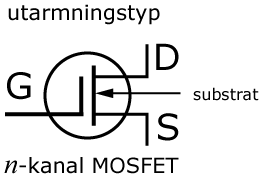
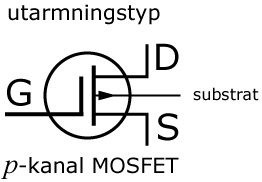
I symbolerna för MOSFET-transistorer av utarmninsgtyp ingår en kondensatorsymbol.
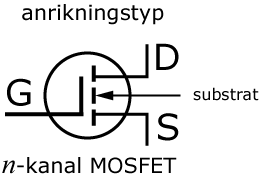
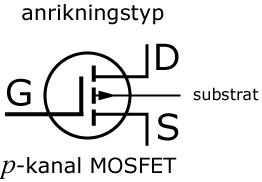
Anrikningstyp
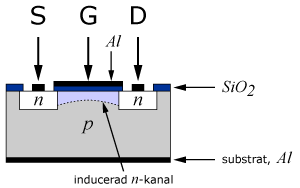
Till skillnad från JFET- och MOSFET-transistorer av utarmningstyp leder MOS-transistorer av anriknikngstyp ingen ström när spänningen på styrelektroden är noll. Transistorns uppbyggnaden framgår av figuren intill. När spänningen på styrelektroden är positiv, attraheras elektroner till området under gate-elektroden och samtidigt repelleras hål bort från denna region. Överskottet av elektroner inducerar en kanal av n-typ under gaten och en förbindelse mellan source och drain uppstår. Den elektriska fältstyrkan orsakad av styrelektroden bestämmer storleken hos den inducerade kanalen, som i sin tur bestämmer strömstyrkan mellan source och drain. När spänningen på styrelektroden är negativ, induceras en positiv laddning och eftersom en av pn-övergångarna mellan source och drain alltid är förspänd i backriktningen kommer ingen ström att kunna flyta mellan dessa elektroder.
Symboler
Den inducerade kanalen under gaten är streckprickad i symbolerna för MOS-transistorer av anriknikngstyp. Pilen har olika riktning beroende på om det är en n-kanals transistor eller en p-kanal.
Operationsförstärkare
I avsnittet om transistorer beskrevs hur en transistor kan fungera som en förstärkare. Kollektorströmmen beror av basströmmen och transistorns strömförstärkningsfaktor. Förstärkare har en särskilt stor betydelse i många elektronik konstruktioner och utgör en nyckelkomponent.
En ideal förstärkare ska ha följande egenskaper:
- Hög inimpedansen Rin = ∞.
- Låg utimpedansen Rut = 0 Ω.
- Hög spänningsförstärkning A = Uut / Uin = ∞.
- Oändlig bandbredd 0 Hz - ∞.
- Perfekt balans d.v.s. Uin = 0 V ger Uut = 0 V.
- Ingen drift orsakad av temperaturvariationer.
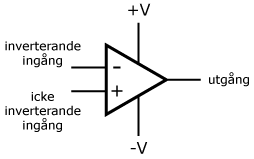
I praktiken går det att realisera en ideal förstärkare närmast genom att använda sig av en operationsförstärkare, vilken förkortas OP-förstärkare eller enbart OP, ibland även OP-amp av engelskans "amplifier". OP-förstärkare tillverkas i form av integrerade kretsar (IC = integrated circuit), vilka är konstruerade av flera interna transistorer. Den interna uppbyggnaden är normalt ointressant, man betraktar en OP-förstärkare som ett byggblock med vissa specifika egenskaper som förstärkning, bandbredd, offset-ström, bias-ström etc.
Operationsförstärkaren är en direktkopplad förstärkare. Grovt kan den beskrivas som en förstärkare med en inverterande och en icke inverterande ingång. Spänningsskillnaden mellan dessa förstärks och normalt har OP-förstärkaren mycket stor förstärkning. Den motkopplas för att ge önskad förstärkning.
Vilket maximalt sving som man kan få på utgången beror på vilka matningssvängningar som används. Tradionellt har man använt +/- 15 V, men numera förekommer det OP-förstärkare med olika användningsområden och matningsspänningar.
Även om man idealt önskar en oändligt stor bandbredd, är det långt ifrån praktiskt möjligt. Bandbredden är normalt ca 100 kHz - 10 MHz. De operationsförstärkare som har större bandbredd (0 - 1 GHz) kallas vanligtvis för videoförstärkare. Spänningsförstärkningen är mycket hög, omkring 105 - 106 ggr.
En OP-förstärkares grafiska symbol.
En OP-förstärkares ingångssteg utgörs oftast av ett differentialsteg, varför man har två ingångar. Plus-ingången uppvisar ingen fasförskjutning mellan insignal och utsignal. Den kallas därför för den icke inverterande ingången. Den andra ingången, minus-ingången ger 180° fasvridning mellan in- och utsignal. Minus-ingången kallas därför för den inverterande ingången.
Inimpedansen kan göras mycket hög genom att man använder bipolära transistorer eller FET-transistorer. Med bipolära transistorer kan OP-förstärkarens inimpedans vara i storleksordningen 100 kΩ upp till 1 MΩ. För FET-transistorer ligger inimpedansen i området 108 - 1015 Ω.
Utimpedansen hos en OP-förstärkare går att få mycket låg beroende på vilken typ av utgångssteg man väljer (vanligtvis GK-steg eller "Push-pull"-steg). Normalt ligger utimpedansen i området 10 - 100 Ω.
Begreppet offset-spänning är den spänning som måste läggas mellan plus- och minusingångarna för att utspänningen skall bli noll. Offset-spänningen beror till största delen på skillnader i de två ingångstransistorernas bas-emitterspänning UBE.
Vanligtvis kan offset-spänningen kompenseras m.h.a. en yttre trimpotentiometer, däremot är det svårare att kompensera för temperaturberoendet. En OP-förstärkare av standardtyp kan ha en temperaturdrift i området 1 - 50 μV/°C.
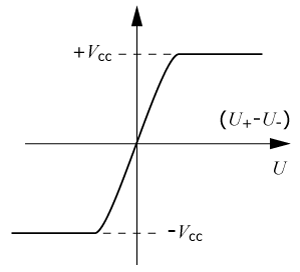
En OP-förstärkares utsignal är proportionell mot spänningsskillnaden mellan plus- och minus-ingångarna multiplicerad med OP:ns råförstärkningen, A. Eftersom råförstärkningen vanligtvis är mycket hög, kommer en mycket liten insignal mellan ingångarna att ge en stor utspänning. Men, en OP-förstärkare kan inte överstiga matningsspänningen, varför förstärkaren mycket snart blir överstyrd när insignalen ökar. OP-förstärkaren lämnar sitt linjära område och når en mättnad, vilket inträffar beroende av råförstärkningen och storleken på matningsspänningens.
OP-förstärkarens överföringsfunktion.
Uut = A·(U+ - U-)
OP-förstärkarens bias-ström är den basström som krävs för att ingångstransistorerna i differentialsteget skall erhålla en lämplig s.k. vilopunkt (även kallad arbetspunkt). På grund av skillnaden i bias-ström mellan de båda ingångstransistorerna kommer utspänningen inte att bli noll. Skillnaden i bias-ström kallas för offset-ström, i normala fall kan den vara på ca 500 nA.
Operationsförstärkare kan i det närmaste betraktas som ideala förstärkare och med lämpliga återkopplingsnät kan de ges olika egenskaper. I princip förekommer det två olika standardkopplingar för operationsförstärkare: inverterande och icke inverterande återkoppling. Förstärkare med rent resistiva återkopplingsnät är inverterare och icke inverterande förstärkare, den sistnämnda kan göras som en spänningsföljare om man önskar en impedansomvandlare till att driva lågohmiga laster. Genom andra resistiva återkopplingar kan en OP-förstärkare fungera som ström/spänningsomvandlare, summatorer och differentialförstärkare. Om man i återkopplingen har kapacitiva komponenter kan OP:n användas som en integrator. Integratorer användes förr i s.k. analogimaskiner till att lösa differentialekvationer. Numera används de nästan uteslutande inom regler- och analog elektronik. Genom att ändra lite i integratorns återkoppling kan man istället få en deriverande förstärkare. Man byter då ut kapacitansen i återkopplingen mot en resistans och sätter kapacitansen på ingången.
Mikroprocessorer
 En mikroprocessor är en programmerbar elektronisk enhet. Den är en integrerad krets (IC) som innefattar funktionerna hos en dators centralenhet, CPU (central processing unit). CPU:n består i huvudsak av fyra delar: styrenhet, ALU (aritmisk/logisk enhet), register och programräknare. Mikroprocessorn tar emot digital data som insignal, behandlar den enligt lagrade programinstruktioner och tillhandahåller resultatet som utsignal.
En mikroprocessor är en programmerbar elektronisk enhet. Den är en integrerad krets (IC) som innefattar funktionerna hos en dators centralenhet, CPU (central processing unit). CPU:n består i huvudsak av fyra delar: styrenhet, ALU (aritmisk/logisk enhet), register och programräknare. Mikroprocessorn tar emot digital data som insignal, behandlar den enligt lagrade programinstruktioner och tillhandahåller resultatet som utsignal.
År 1971 lanserades de första mikroprocessorerna. Tre olika projekt levererade var sin mikroprocessor ungefär samtidigt samma år: Intel's 4004, Texas Instrument's (TI) TMS 1000 och Garrett AiResearch's Central Air Data Computer (CADC) och MP944. Bortsett från CADC:n som hade 20 bitar, hade de tidiga processorerna 4 bitars ordlängd. Ganska snart kom processorer med 8 bitar, och på 1990-talet hade ordlängden ökat till 64-bitar. Kapaciteten för mikroprocessorer har sedan introduktionen haft en enorm utveckling. De första mikroprocessorerna som togs fram på 1970-talet hade haft klockfrekvenser på omkring 500 kHz, och var konstruerade med runt 3000 antal transistorer. 2014 låg klockfrekvensen på ca 2,5–5 GHz och antalet transistorer var då omkring 4,2 miljarder stycken. Samtidigt har teknikutvecklingen möjliggjort en kraftig reduktion av de geometriska måtten. På 1970-talet gjordes linjebredder på ca 10 μm, 2014 hade de minskat till 22 nm. Datorers prestanda har också förbättrats genom multi konstruktioner där man använder extra processorkärnor s.k. multi-core processorer. Varje kärna kan då samtidigt köra processorinstruktioner parallellt.
Den expansiva utvecklingen, med alltmer effektiva tillverkningsmetoder och höga produktionsvolymer, har inneburit att priserna på elektronikkomponenter har kunnat pressas ner. Denna enorma tillgång på billiga datorer i integrerade kretsar har medfört en total förändring av det moderna samhället. Generella mikroprocessorer i persondatorer används för beräkning, textredigering, multimedia displayer och kommunikation över Internet. Det förekommer mängder av mikroprocessorer i inbyggda system, vilket ger digital kontroll över otaliga föremål från apparater till bilar, mobiltelefoner och industriell processtyrning. År 2008 tillverkades det ca tio miljarder CPU processorer och av dem användes 98 % i inbäddad elektronik.
Likström
Spänningskällor och elektromotorisk kraft (emk)
En likriktad ström, där laddningsbärare förflyttar sig i en och samma riktning, kallas för en likström. Om man ska driva en ström i en ledare krävs det en potentialskillnad mellan ledarens ändpunkter. Ledaren måste därför anslutas till en spänningskälla. Karaktäristiskt för en spänningskälla är dess elektromotoriska kraft (emk) eller elektromotoriska spänning (ems) som upprätthåller en potentialskillnad, den s.k. polspänningen, mellan spänningskällans två poler. Vid belastning, med t.ex. en resistor, avges elenergi och polspänningen sjunker. Hos en obelastad energikälla är polspänningen lika med källspänningen som betecknas med bokstaven E.
Elekromotorisk spänning kan uppstå på ett flertal olika sätt. Det kan uppstå en ems i övergången mellan en elektrolyt och en metallyta, vilket utnyttjas i galvaniska element som t.ex. batterier, ackumulatorer eller bränsleceller. Ett annat vanligt förekommande sätt är med hjälp av induktion, då en inducerad spänning skapas när en elektrisk slinga och ett magnetfält förflyttas i förhållande till varandra. Elektriska generatorer bygger på denna princip.
En spänningskälla som är ansluten till en krets driver en ström från den positiva polen till den negativa polen. Det finns olika kretssymboler som illustrerar en emk. Det är inte nödvändigt att sätta ut tecknen eller spänningspilen eftersom den längre linjen alltid anger spänningskällans positiva pol.
Ohms lag

Samband mellan olika elektriska storheter baserat på Ohms och Joules lagar.
En enkel elektrisk krets består av en spänningskälla med polspänningen U som driver strömmen I genom ett motstånd med resistansen R. Strömmen i kretsen beror av spänningen, där förhållande mellan dessa storheter är linjärt. Under förutsättning att temperaturen är konstant kommer kvoten mellan U och I att vara konstant. Denna kvot utgör värdet av kretsens resistans. Sambandet mellan spänning, ström och resistans kallas för Ohms lag och skrivs vanligtvis på följande form:
U = R I
(Ohms lag)
Joules lag
En elektrisk ström som passerar i en metallisk ledare ger upphov till en värmeutveckling, orsakad av ledningselektronernas kollition med metallens gitteratatomer. Det sker alltså en energiomvandling i ledaren, vilket innebär att det åtgår elektrisk energi för att driva en ström genom ledaren. Potentialskillnaden (spänningen) U är definierad som det arbete W som det elektriska fältet åstadkommer per enhetsladdning Q.
Elektrisk effekt är mängden energi per tidsenhet och tillsammans med ovanstående samband för spänning ges att effekten P är en produkt av spänningen U och strömmen I.
Detta samband kan även beskrivas med resistansen R genom att tillämpa Ohms lag. Förhållandet kallas för Joules lag.
Seriekoppling och parallellkoppling av motstånd
Seriekoppling
I en krets med seriekopplade resistorer är motstånden kopplade i följd efter varandra längs en gemensam strömslinga. Den ström som passerar i kretsen är densamma för alla resistorer. Spänningskällans spänning fördelar sig och ger spänningsfall över de olika resistorerna enligt Ohms lag. Den totala resistansen Rtot i kretsen motsvarar summan av alla delresistanser.
Den totala resistansen Rtot för de seriekopplade resistorerna i figuren kan beräknas enligt
Rtot = R1 + R2 + R3
Den totala resistansen i en krets med seriekopplade resistorer kan med ett allmänt uttryck skrivas
Parallellkoppling
Parallellkoppling innebär att motstånden är kopplade så att huvudströmmen I0 delar upp sig på de olika resistanserna. Spänningen i en parallellkopplad krets kommer att vara samma över alla motstånden och lika spänningskällans utspänning. Huvudströmmen I delar sig enligt Ohms lag i de olika resistanserna.
I en krets med parallellkoppling är den totala resistansens inverterade värde lika med summan av de ingående resistansernas inverterade värden.
Ett mer allmänt uttryck för parallellkoppling av N stycken motstånd skrivs
Kirchoffs lagar
Kirchoffs första lag:
I en elektrisk krets som har ledare som förgrenar sig, är summan av de strömmar som flyter till och från en förgreningspunkt lika med noll. Med en förgreningspunkt menas en sammankoppling av tre eller flera ledare. Strömmar med riktning in mot en knutpunkt räknas som positiva, och strömmar som går från förgreningspunkten räknas som negativa.
(Kirchoffs strömlag)
Exempel:
I0 + I1 + I2 = 0
Kirchoffs andra lag:
I ett elektriskt nät är summan av alla potentialändringar i varje sluten krets eller slinga lika med noll.
(Kirchoffs spänningslag)
Exempel:
U0 + U1 + U2 = 0
Thévenins teorem
En tvåpol kan funktionsmässigt ersättas med en spänningskälla i serie med en resistans, där spänningen är lika med tvåpolens tomgångsspänning och resistansen är lika med den inre resistansen hos tvåpolen.
Tvåpolens tomgånggspänning erhålls som spänningen på dess utgång och beräknas när utgången inte är belastad med en extern last. Den inre resistansen motsvarar den resistans, som kan mätas eller beräknas mellan tvåpolens poler. För att kunna beräkna tvåpolens inre resistans avlägsnar man alla spänningskällor och ersätter dem med kortslutningar, eftersom ideala emk:er har en inre resistans som är lika med noll.
Nortons teorem
Ett nät bestående av spänningskällor och resistorer kan ersättas med en strömgenerator parallell med tvåpolens inre resistans.
Strömgeneratorn är en ideal strömkälla som har en oändlig inre resistans och levererar en konstant ström. Strömgeneratorns strömvärde motsvaras av kortslutningsströmmen Ik hos tvåpolen och den inre resistansen beräknas på motsvarande sätt som i Thévenins teorem.
Kortslutningsströmmen kan skrivas som
där E motsvarar tomgångsspänningen för kretsen på precis samma sätt som för Thévenins teorem.
Växelspänning och växelström
Radianer (rad)
En radian (rad) är den härledda SI-enheten för vinklar. Radianer är vanliga i vetenskapliga och tekniska sammanhang eftersom det är ett matematiskt mer naturligt mått än vad grader är.
En vinkels mått i radianer är definierad som den sträcka utmed enhetscirkelns rand som spänns upp av vinkeln. Då enhetscirkeln har radien 1 blir dess omkrets 2π. Ett varv = 360 grader = 2π rad. Annorlunda uttryckt, 1 rad ≈ 57,296 grader.
Generering av en sinusformad växelspänning
Växelspänning har blivit standard i det allmänna elnätet därför att den underlättar kraftöverföring över långa sträckor. Fördelen ligger i att växelspänningen är enkel att omvandla. Energi kan transporteras via högspänningsledningar med relativt små överföringsförluster, och sedan transformeras till lämplig spänning anpassad för olika behov.
En växelspänning ändrar ständigt sin storlek och polaritet. För att beskriva hur en växelspänning genereras kan man betrakta en flat, rektangulär spole placerad i ett homogent magnetfält. Enligt induktionslagen skapas en inducerad spänning då en ledare eller ett magnetiskt flöde förflyttas i relation till varandra. När spolen roterar kring sin egen axel generas det således en spänning som bestäms av den magnetiska flödesändringen per tidsenhet (Faradays lag). Den flödesmängd som träffar spolen ändras ständigt från att vara som störst då spolen befinner sig i ett läge vinkelrätt mot magnetfältet, till att inget flöde passerar när spolen är parallell med fältet. även om spolens rotationshastigheten är densamma, kommer flödesändringen per tidsenhet att variera. Den inducerade spänningen följer denna variation, ju snabbare flödesförändringen är desto högre blir spänningen. Hur den inducerade spänningen varierar med tiden för en spole som roterar med konstant hastighet, kan förklaras utifrån olika samband. I uttrycken används följande beteckningar:
B = magnetiska flödestätheten [T] A = spolens area [m2] Φ = magnetiska flödet [Wb] eller [Vs] t = tid [s] ω = spolens vinkelhastighet [rad/s] ωt = spolens tidsvinkel eller fas [rad] α = spolens faskonstant [rad] ωt + α = spolens momentanvinkel [rad] f = spolens varvtal [Hz] T = spolens omloppstid, perioden (1/f) [s] N = antalet lindningsvarv på spolen [varv] u = den inducerade spänningens momentanvärde [V] U0 = spänningens amplitudvärde eller toppvärde [V]

Tvärsnittsvy av en flat, rektangulär spole som roterar i ett homogent magnetfält.
Antag att spolens utgångsläge är vinkelrätt mot magnetfältets flödestäthet. Den roterande spolen kommer efter tiden t att ha vridits vinkeln ωt. Det magnetiska flöde som spolen utsätts för, kan då beskrivas med
Φ = B A cos ωt
Den inducerade spänningen i spolen beskrivs med uttrycket från induktionslagen
Bokstaven e betecknar den inducerade spänningen. Inom växelströmsläran brukar istället bokstaven u användas och är då det värde som den inducerade spänningen antar i varje ögonblick. I ovanstånde uttryck då det magnetiska flödet Φ deriveras med avseende på tiden t finner man att den inducerade spänningens momentanvärde u är en sinusfunktion av tiden
u = N B A ω sin ωt
Det största magnetiska flöde Φmax som spolen utsätts för under sin rotationsbana, inträffar då spolens area A befinner sig vinkelrätt mot den magnetiska flödestätheten B, vilket här sker då vinkeln ωt = 0 (+ n 2π rad). Eftersom cos 0 = 1, kan det maximala flödet skrivas som produkten av konstanterna B och A.
Φmax = B A
Av detta framgår att den maximala momentanspänningen som induceras i spolen är
umax = N Φmax ω (sin ωt = 1)
Detta värde erhålls när den magnetiska flödesförändringen per tidsenhet är som störst, vilket sker då spolen befinner sig parallellt med det magnetiska fältets flödesriktning. Då når den inducerade spänningen sitt toppvärde eller amplitudvärde som brukar betecknas med U0, andra tecken kan vara |U| eller Û. Det maximala värdet på den inducerade spänningen kan alltså skrivas
U0 = N B A ω.
Spänningens amplitudvärde tillsammans med spolens tidsvinkel är vad man behöver känna till för att beskriva den inducerade spänningen i varje tidpunkt
u = U0 sin ωt.
Spänningen kan även uttryckas på former där man utnyttjar sambanden mellan vinkelhastigheten ω, frekvensen f och perioden T.
ω = 2π f ⇒ u = U0 sin 2π f t ω = 2π /T ⇒ u = U0 sin (2π /T) t
Ovanstående uttryck gäller då spolens utgångsläge är vinkelrätt magnetfältet. En mer allmän formel för spänningens momentanvärde, där man tar hänsyn till en fasförskjutning av sinusfunktionen, erhålls genom
u(t) = U0 sin (ωt + α).
I ett visardiagram återges den sinusformade växelspänningens tidsberoende. En visare, vars längd är proportionell mot växelspänningens amplitudvärde U0, får rotera moturs kring punkten 0 med vinkelhastigheten ω. Efter tiden t har visaren vridit sig vinkeln ωt. Visarens projektion på ordinataxeln anger spänningens momentanvärde. En sinusformad växelspänning kan vara fasförskjuten, men benämns ändå sinusformad.

Växelström
I avsnittet om generering av en sinusformad växelspänning beskrevs hur en spole som roterar i ett magnetfält ger upphov till en periodiskt varierad spänning. Om spolen ingår i en sluten strömkrets kommer även strömmen att växelvis ändra sin riktning. Det uppstår en växelström. Vid en växelström oscillerar elektroner fram och tillbaka, och det sker egentligen inte någon laddningstransport. En sinusströms momentanvärde i bestäms ur
i(t) = I0 sin (ωt + β),
där I0 är strömmens amplitud, ωt är tidsvinkeln och β är strömmens faskonstant.
Effektivvärde
Effektivvärdet Ieff av en periodisk växelström motsvarar värdet av den likström, som i en resistor ger en effektutveckling lika stor som växelströmmens medeleffektutveckling i den givna resistorn.
En växelström som passerar genom ett motstånd, ger under en period energiutvecklingen
En likström I skapar under samma tid en energi i motståndet som kan skrivas
Dessa uttryck skall enligt definitionen vara lika
Vilket för en sinusformad växelström innebär att strömmens effektivvärde Ieff är lika med toppvärdet dividerat med √2, och motsvarande samband gäller för effektivvärdet av en sinusformad växelspänning.
Resistans, kapacitans och induktans i växelströmskretsar
Om man betraktar ett mycket litet tidsintervall, kan växelströmmen behandlas som en likström. Ohms och Kirschoffs lagar kan därför tillämpas när det gäller ögonblicksvärden (momentanvärden) hos spänningar och strömmar. I växelströmskretsar är resistorer, kondensatorer och spolar passiva komponenter som (i det idealiserade fallet) har resistans R, kapacitans C och induktans L.
Resistans
För en resistans gäller Ohms lag för både momentanvärden och för toppvärden hos växelströmmen. Spänningens momentanvärde erhålls av
u = R i
där u är växelspänningens momentanvärde, i är växelströmmens momentanvärde och R utgör resistansen.
Om strömmen genom en resistans motsvaras av en sinusformad växelström:
i = I0 sin ωt
kommer spänningen då att bli
u = R I0 sin ωt = U0 sin ωt ⇒ R I0 = U0
Växelströmmen genom en resistans och växelspänningen över den är i fas med varandra.
Kapacitans
Kapacitans beskriver förmågan att lagra elektrisk laddning och är definierad som kvoten mellan den laddningsmängd som kan lagras i en kondensator och den pålagda spänningen. För att förklara vad som sker med ström och spänning då man ansluter en växelspänning till kondensatorn, kan man betrakta en enkel kapacitiv krets bestående av en kondensator kopplad till en växelspänning. Antag att laddspänningen är en sinusformad växelspänning u och väljs som riktfas kan den uttryckas med funktionen
u = U0 sin ωt,
Kondensatorns momentana laddning betecknas med q, dess kapacitans med C och spänningen över kondensatorn betecknas med uc. Mellan dessa storheter gäller sambandet
q = C uc
Under tiden dt tillförs laddningen dq = i dt. Då kapacitansen är konstant, kan man genom att derivera uttrycket ovan med avseende på tiden skriva
Enligt Kirchhoffs spänningslag är summan av alla potentialändringar som ingår i en sluten krets lika med noll. Summerar man spänningsskillnaderna i denna krets erhåller man
u - uc = 0
Dessa samband ger
⇒
Genom derivering av växelspänningen med avseende på tiden kan man skriva strömmen som
i(t) = C ω U0 cos ωt
Sinus- och cosinusfunktioner kan uttryckas i varandra, eftersom de är samma funktioner som endast skiljer sig åt med en fasförskjutning av π/2. För att lättare kunna jämföra med fasen i uttrycket för spänningen skrivs växelströmmen som en sinusfunktion, och ser då ut så här
i(t) = C ω U0 sin (ωt + π/2 )
där
C ω U0 = I0
Om man jämför fasuttrycken för växelströmmen och växelspänningen över kondensatorn, framgår det att strömmens fas är π/2 rad större än spänningens, vilket innebär att strömmen kommer att nå sitt toppvärde I0 före spänningen. Fasförskjutningen är i detta fall kapacitiv.
Induktans
När en elektrisk ström passerar genom en spoles lindning alstras ett magnetfält i spolen. Om strömmen och därmed flödet i spolen ändras, induceras en spänning och denna har en sådan riktning, att strömändringen motverkas enligt Lentz' lag. Den inducerade spänningen e ges av formeln
där L är spolens induktans, i är strömmen och t är tiden. En växelström som skickas genom en spole ger alltså upphov till en inducerad spänning som söker motverka strömändringarna. Detta medför att strömmen genom spolen och spänningen över den inte är i fas med varandra, vilket kan beskrivas genom att analysera sambanden i en enkel krets bestående av en spole kopplad till en växelspänning. Om strömmen i kretsen är en sinusformad växelström enligt uttrycket
i = I0 sin ωt,
I ett visst ögonblick då strömmen är växande ger en potentialvandring i kretsen
u - uL = 0
En derivering av växelströmmen med avseende på tiden ger spänningen
u = uL = ω L I0 cos ωt
För en jämförelse av fasuttrycken mellan ström och spänning skrivs växelspänningen istället som en sinusfunktion
uL = ω L I0 sin (ωt + π/2)
där växelspänningens toppvärde är
U0 = ω L I0
Växelspänningen över spolen är fasförskjuten π/2 rad före strömmen. Detta innebär att spänningen kommer att nå sitt toppvärde U0 före strömmen. Fasförskjutningen är i detta fall induktiv.
RLC-krets i visardiagram
Potentialskillnaderna över de tre seriekopplade komponenterna i en RLC-krets kan illustreras med hjälp av ett visardiagram, där spänningarnas momentanvärden, samt fasförskjutningen mellan spänning och ström går att avläsa.
I visardiagrammet beskrivs sinusspänningen som en roterande visare U, vars längd motsvarar amplitudvärdet hos spänningen. Visaren roterar motsols med vinkelhastigheten ω och när tiden t ökar, så ökar också tidsvinkeln ωt till referensstrålen på x-axeln. Momentanvärdet u(t) kan man avläsa som visarspetsens projektion på y-axeln (y-koordinaten). Motsvarande gäller för strömmen.
Eftersom komponenterna i RLC-kretsen är seriekopplade, så är strömmen genom dem lika och väljs därför som riktfas. Om växelströmmen är sinusformad erhålls ström och spänningars momentanvärden av sambanden
i = I0 sinωt u = U0 sin(ωt + φ)
Spänningen U0R över motståndet kommer att vara i fas med strömmen.
U0R = I0 R ⇒ uR = I0 R sinωt
Spänningen U0L över spolen är fasförskjuten π/2 rad före strömmen.
U0L = I0 ωL ⇒ uL = I0 ωL sin(ωt + π/2)
Spänningen U0C över kondensatorn är fasförskjuten π/2 rad efter strömmen.
U0C = I0/ωC ⇒ uC = (I0/ωC) sin(ωt - π/2)
Summan av spänningsfallen över de tre komponenterna ger kretsens totala momentanspänning u.
u = uR + uL + uC
Med hjälp av visardiagrammet kan spänningarna adderas. Strömmen är riktfas, och ett godtyckligt värde väljs på fasuttrycket ωt. Spänningsvisaren U0R riktas längs strömvisaren. Spänningsvisaren U0L är π/2 rad före strömvisaren, och spänningsvisaren U0C är π/2 rad efter strömmen. Eftersom spänningarna U0L och U0C är på en rät linje och riktade åt motsatt håll adderas dessa först, vilket ger
U0L + U0C = I0 (ωL - 1/ωC)
Genom vektoriell addition av spänningsvisarna U0L - U0C och U0R erhålls visaren med spänningsamplituden U0. Med Pythagoras sats erhålls följande uttryck för spänningsamplituden
Ur visardiagrammet kan man här bestämma spänningens momentanvärde genom att projicera visaren U0 på ordinataxeln.
u = U0 sin(ωt + φ)
Ett uttryck för fasförskjutningen mellan strömmen och spänningen kan visardiagrammet också ge.
Reaktans (X)
Storheten reaktans beskriver ett slags frekvensberoende elektriskt motstånd och definieras på samma sätt som resistansen vid likström. Reaktans har beteckningen X och motsvarar resistansen R i en rent resistiv krets vad gäller den strömbegränsande verkan. Enheten för reaktans är en Ohm, 1 Ω.
Kapacitiv reaktans, Xc
I en enkel kapacitiv krets med en kondensator som är ansluten till en växelspänning, kan strömmens toppvärde I0 uttryckas som produkten av vinkelhastigheten ω, kapacitansen C och spänningens amplitudvärde U0.
I0 = ω C U0
Genom att jämföra ovanstående uttryck med Ohms lag, U = R I, kan kondensatorns reaktans Xc definieras.
Induktiv reaktans, XL
I en induktiv krets där en spole är ansluten till en växelspänning motsvaras spänningens toppvärde av
U0 = ω L I0
Reaktansen för en spole har beteckningen XL och precis som med reaktansen hos en kondensator kan man genom en jämförelse med Ohms lag definiera spolens reaktans.
Impedans (Z)
RLC-krets
En RLC-krets bestående av ett motstånd, med resistansen R, i serie med en spole, med induktansen L, och en kondensator, med kapacitansen C, drivs av en sinusformad växelspänning u, med vinkelhastigheten ω. över motståndet är ström och spänning i fas, medan över spolen och kondensatorn kommer spänningen att vara fasförskjuten π/2 rad. För spolen är fasförskjutningen induktiv, då spänningen når sitt toppvärde före strömmen. över kondensatorn däremot, är fasförskjutningen kapacitiv, då spänningens toppvärde kommer efter strömmens. Spänningens toppvärde kan uttryckas med formeln
Genom att jämföra uttrycket ovan med Ohms lag, U = R I, framgår det att den resistiva faktorn i sambandet utgörs av ett komplext tal. Denna komplexa del är definierad som kretsens impedans, vilken betecknas med bokstaven Z och har enheten en Ohm, 1 Ω.
Imaginära och komplexa tal
Inom matematiken finns det en grupp av tal som kallas imaginära tal. Ett imaginärt tal är ett tal vars kvadrat är ett negativt reellt tal. Imaginära tal brukar betecknas med bokstaven i, men för att undvika förväxling med beteckningen för strömstyrkans momentanvärde i används inom elläran vanligtvis bokstaven j. Det imaginära talet j är definierat som
j2 = -1 ⇔ j = √-1
Ett reellt tal och ett imaginärt tal kan kombineras till ett komplext tal, som skrivs på formen
z = x + j y
där x utgör realdelen och y är imaginärdelen av det komplexa talet z.
Komplexa tal kan illustraras grafiskt i ett komplext talplan bestående av en realaxel (Re) och en imaginäraxel (Im). Addition av komplexa tal kan åskådliggöras genom att de representeras som vektorer i det komplexa talplanet. Komplexa tal adderas vektoriellt på samma sätt som visare.
Koordinaterna x respektive y i ett komplext tal kan även visas med polär representation. Utifrån definitionerna för cosinus och sinus för fasvinkeln φ mellan den reella axeln och radius vektorn r alt. |Z|(= vektorn med amplitudbeloppet).
Om man jämför potensserierna för sin(x) och cos(x) med potensserierna för ex erhåller man följande samband:
e jφ = cos φ + j sin φ (Eulers formel)
Detta uttryck kallas för Eulers formel och utgör en av de viktigaste sambanden för komplexa tal. Ett komplext tal kan alltså skrivas i form av en summa eller som en produkt.
z = x + j y = r (cos φ + j sin φ) = r e jφ
jω-metoden
Vid beräkning och dimensionering av växelströmskretsar måste man förutom spänningar, strömmar och resistanser, också ta hänsyn till kretsens induktanser och kapacitanser. En betydande storhet som dessutom ingår i växelströmsteorin är tiden, varför man söker metoder där tiden ej förekommer. Det finns i huvudsak två sätt som ger en enkel tidsoberoende behandling av växelströmskretsar: den grafiska metoden med visardiagram och den symboliska metoden som man vanligtvis kallar jω-metoden.
Först en definition över de ingående beteckningar som används i förklaringen av jω-metoden.
Följande steg sammanfattar jω-metoden:
- Resistanser, kapacitanser och induktanser ersätts med sina komplexa impedanser: R, 1/(jωC) resp. jωL.
- Beräkningar av kretsen görs som om den vore en likströmskrets, m.h.a. Ohms lag och Kirchoffs lagar.
- Välj en känd ström eller spänning som utgångspunkt för beräkningarna. Okända strömmar eller spänningar uttrycks i den kända strömmen eller spänningen.
- Lösningen ger komplexa uttryck för strömmen eller spänningen, av typen:
Ur vilken kan beräknas amplitud |I|, fasskillnad φ, impedans Z, tidsberoendet Re(I) eller Im(I) enligt:
Amplitud: Fasskillnad: Impedans: Strömmen på polär form: Ögonblicksvärden ges av: eller:
Amplitud: Fasskillnad: Impedans: Strömmen på polär form: Ögonblicksvärden ges av: eller:
Källor: wikipedia.org. "Ellära" del 1, 2 och 3, Natura läromedel. "Analogteknik 1", M Gustafsson. "Fysik Gy, grundbok 2:1 och 2:2", Lindkvist Åkerlind Knall. "Elkunskap för vardagsbruk", FERA. "Elektromagnetism", L A Engström. "Faktasidor om elektronik", Elfa Distrelec, "Datorteknik - med inriktning mot 68HC11", Per Dagermo.